Question

30 балов
(Бали: 12)

1) З точки до прямої проведено дві похилі, довжини яких дорівнюють 17 см і 10 см. Проекції цих похилих на пряму відносяться, як 5:2. Знайдіть довжину спільного перпендикуляра.

2) У рівнобедреному трикутнику ABC AC – основа, – висота. Знайдіть висоту, проведену з вершини B, якщо AD=20 см.

3) У гострокутному трикутнику АВС АС=15 см, ВС=14 см. АК і ВМ - висоти трикутника, ВМ =11,2 см. Знайдіть синус, косинус і тангенс кута С трикутника АВС.

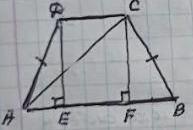
4) Основи рівнобічної трапеції дорівнюють 1 см і 7 см, а бічна сторона дорівнює 5 см. Знайдіть діагональ трапеції.

5) Периметр рівнобедреного трикутника дорівнює 10 см, а основа відноситься до бічної сторони, як 1:2. Знайдіть довжину медіани, проведеної до основи.

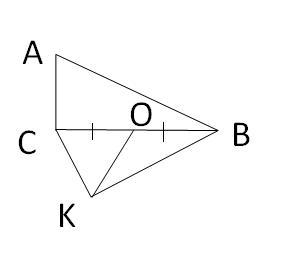
6) Знайдіть AB, якщо ∠ACB =∠CKB = 90°, ∠A=α, KO=a.

Answer 1

Ответ:

Объяснение:

1) L₁=17 см;

L₂=10 см;

L₁ₓ/L₂ₓ=5/2  

h   ?   h²=17²-(5x)²=10²-(2x)²; 21x²=189; x=3 см;  h=√(100-4*x²)=

√(100-4*3²)=8 см;

2. надо уточнить условие

3. АС=15 см;

ВС=14 см;

ВМ=11,2 см;

АК⊥СВ;

ВМ⊥АС;        

cosC, sinC,  tgC   ?   sinC=AK/AC; AK=2*S/BC=AC*BM/BC=

15*11,2/14=12 см; sinC=12/15=0,8; cosC=√(1-sin²C)=√(1-0,8²C)=0,6;  

tgC= sinC/cosC=0,8/0,6=4/3;

4) СD=1 см;

AB=7 см;

AD=BC=5 см.    

AC  ?   EF=CD; AE=FB=(AB-EF)/2=(7-1)/2=3 см; CF=

√(BC²-FB²)=√(5²-3²)=4 см; AF=AB-FD=7-3=4 см; AC=√(AF²+CF²)=√(4²+4²)=4√2 см;

5. P=10 см;

a/b=1/2;   b=2a;    

m   ?  m=√b²-(a/2)²;  p=a+2b=a+2*2a=5a ⇒ a=10/5=2 см;  b=2*2=4 см; m=√(4²-(2/2)²)=√15 см;

6.  ∠ACB =∠CKB = 90°,

∠A=α, СО=ВО

KO=a;                            

AB   ?    AB=BC/sinA=BC/sinα; KO - медiана дорiвнюэ 1/2 гiпотенузи = а ⇒ ВС=2а; AB=2а/sinα