Question

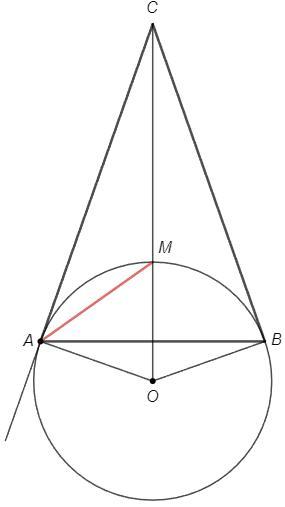
AB-основание равнобедренного треугольника ABC. Докажите что окружность касающаяся сторон угла ACB в точках A и B проходит через точку M-центр вписанной окружности в треугольник ABC.

Answer 1

△ACO=△BCO по трем сторонам => CO - биссектриса ∠ACB и ∠AOB

Окружность пересекает CO в точке M

M - середина дуги AB, ◡AM=◡MB

∠CAM=◡AM/2 (угол между касательной и хордой)

∠BAM=◡MB/2 (вписанный угол)

=> ∠CAM=∠BAM, AM - биссектриса ∠CAB

M - точка пересечения биссектрис △ABC - центр вписанной окружности.