Предмет: Математика,
автор: fffffscmfff
Помогите пожалуйста дам 50 балов (полная роспись задач)
Приложения:
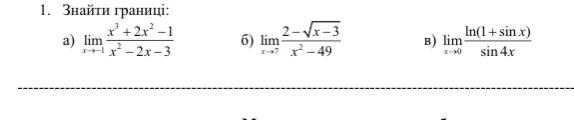
Ответы
Автор ответа:
1
Решение.
Найти пределы функций . Раскрытие неопределённости вида .
Применяем метод разложения на множители, домножение на сопряжённое выражение и замену бесконечно малых эквивалентными .
Похожие вопросы
Предмет: Физика,
автор: ajgerimtoktobaeva23
Предмет: Литература,
автор: z02636526
Предмет: Алгебра,
автор: lapka9889
Предмет: Математика,
автор: lizak8207
Предмет: География,
автор: yulia11makarevych