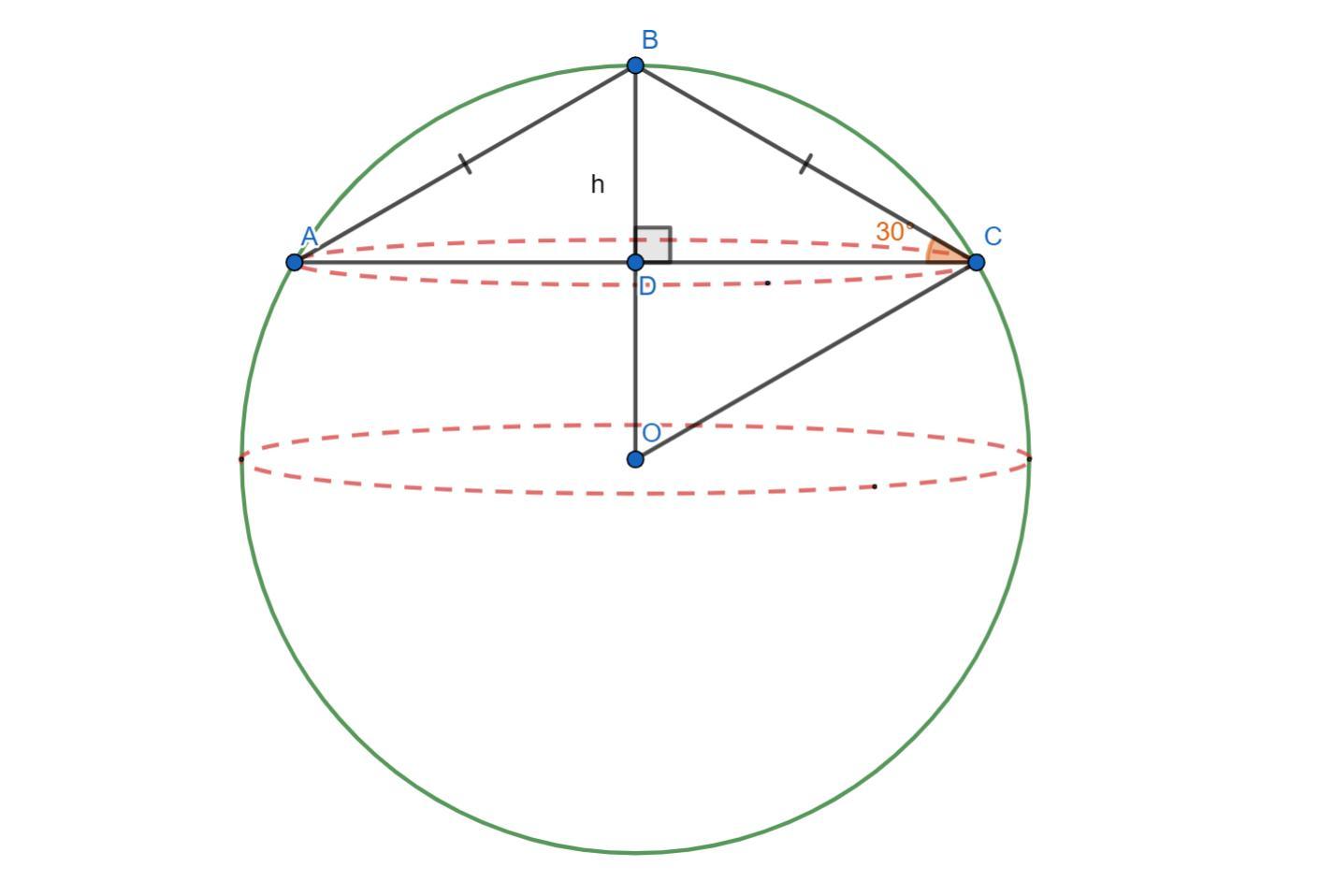
У кулю вписано конус, площа бічної поверхні якого дорівнює 8π√3 см², а твірна нахилена до площини основи під кутом 30°. Знайдіть об’єм цієї кулі.
Ответы
Ответ:
Объем сферы равен (см)³
Объяснение:
Дано :
Sбок.конуса = 8π√3 см²
Rсф = ? , Sсф = ?
Пусть осевым сечением данного конуса будет равнобедренный ΔABC с высотой h = BD , соответственно сторона BC будет являться образующей данного конуса.
Рассмотрим прямоугольный ΔBDC
∠CBO + ∠DCB = 90° ⇒ ∠CBO = 90° - ∠DCB = 90° - 30° = 60°
А поскольку BO = OC как радиусы сферы и ∠CBO = 60° ⇒ ΔBCO равносторонний ⇒ OB = BC = CO из этого мы можем понять , что образующая конуса равна радиусу окружности
Высота (h) конуса лежит против угла в 30° , а катет лежащий против угла в 30° равен половине гипотенузы , то наклонная BC = 2h
Найдем радиус конуса (DC) , по теореме Пифагора
BD² + DC² = BC²
h² + DC² = (2h)²
DC = h√3
По условию нам известно , что Sбок.конуса = 8π√3 см²
Вспомним :
Sбок.пов = πrl - площадь боковой поверхности прямого конуса , где r - радиус основания , l - образующая
Подставим r = h√3 , l = 2h
π·h√3·2h = 8π√3
h² = 4
h = 2 см ⇒ BC =2h = 4 см
Т.к образующая равна радиусу сферы , то R = BC = 4 см
Находим объем сферы по формуле
(см)³
#SPJ1