Хорда кола перетинає його діаметр під кутом 30 градусів і ділиться діаметром на відрізки завдовжки 4 см і 7 см.Знайдіть відстань від кінців хорди до прямої,що містить діаметр кола. ДАЮ 75 БАЛЛОВ СРОЧНО ПОЖАЛУЙСТА
Ответы
Ответ:
Відстані від кінців хорди до прямої,що містить діаметр кола дорівнюють 3,5 см і 2 см
Объяснение:
Хорда кола перетинає його діаметр під кутом 30 градусів і ділиться діаметром на відрізки завдовжки 4 см і 7 см. Знайдіть відстань від кінців хорди до прямої,що містить діаметр кола.
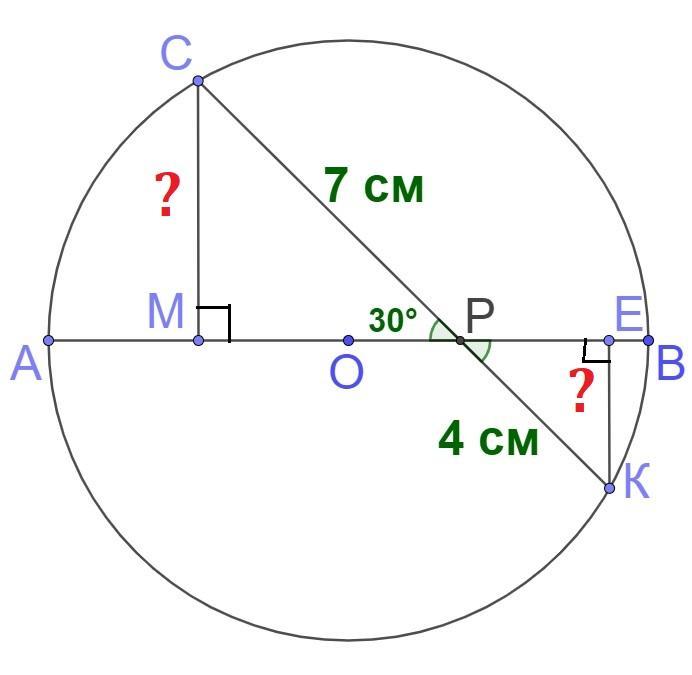
За умовою маємо коло з центром у точці О, АВ - діаметр кола. Хорда СК перетинає АВ у точці Р. СР=7 см, РК=4 см, ∠СРМ=30°
СМ⊥АВ ⇒ СМ - відстань від точці С до діаметра кола
КЕ⊥АВ ⇒ ЕК - відстань від точці С до діаметра кола
Знайдемо СМ і ЕК.
1. Розглянемо прямокутний трикутник СРМ(∠М=90°)
Катет СМ лежить напроти кута ∠СРМ=30°, тому він дорівнює половині гіпотенузи СР (за властивістю).
СМ=1/2 · СР=1/2·7=3,5(см)
2. Розглянемо прямокутний трикутник КРЕ(∠Е=90°)
∠КРЕ=∠СРМ=30° - як вертикальні кути
ЕК=1/2·РК=1/2·4=2(см) - за властивістю катета, що лежить проти кута 30°
Відповідь: 3,5 см, 2 см
#SPJ1