Срочно Геомерія 8 класс 30 балів
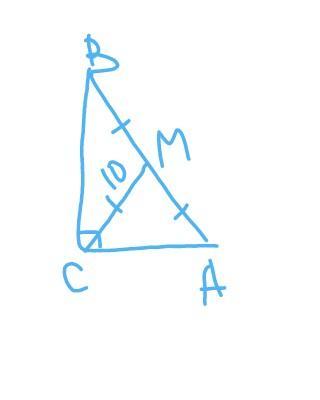
Медіана, проведена до гіпотенузи прямокутного трикутника, дорівнює 10 см. Знайдіть сторони трикутника, якщо різниця його катетів дорівнюс 4 см.
Если нужен перевод скажите
Ответы
Ответ:
Позначимо катети прямокутного трикутника як x та x+4 (за умовою їх різниці дорівнює 4 см). Позначимо гіпотенузу як c.
Згідно з властивостями прямокутних трикутників, медіана, проведена до гіпотенузи, ділить її на дві рівні частини. Отже, медіана має довжину, рівну половині гіпотенузи:
10 см = c/2
c = 20 см
Застосовуючи теорему Піфагора, ми можемо записати:
x^2 + (x+4)^2 = 20^2
Розв'язавши це рівняння, ми знаходимо:
x^2 + x^2 + 8x + 16 = 400
2x^2 + 8x - 384 = 0
x^2 + 4x - 192 = 0
(x+16)(x-12) = 0
Отже, x = 12 (позитивний корінь, оскільки x представляє довжину сторони трикутника).
Таким чином, сторони прямокутного трикутника дорівнюють 12 см та 16 см (згідно з умовою, різниця між катетами дорівнює 4 см).
Объяснение:
∆АВС ; ∠С=90° ; медиана СМ=10 см
ВС-АС=4 см
найти: АС ; ВС ; АВ
решение:
АВ=2•СМ=2•10=20 см
ВС-АС=4 см => ВС=4+АС;
По теореме Пифагора:
АВ²=АС²+ВС²
20²=АС²+(4+АС)²
400=АС²+16+8АС+АС²
-2АС²-8АС+384=0
-АС²-4АС+192=0
АС²+4АС-192=0
D=4²-4•1•(-192)=16+768=784
AC=(-4-28)/2= -16 не подходит
АС=(-4+28)/2=12 см
ВС=4+12=16 см
ответ: АС=12 см ; ВС=16 см ; АВ=20 см