Найти площадь фигуры которая ограничена линиями
1)у=–2х, у=корень(х), у=2
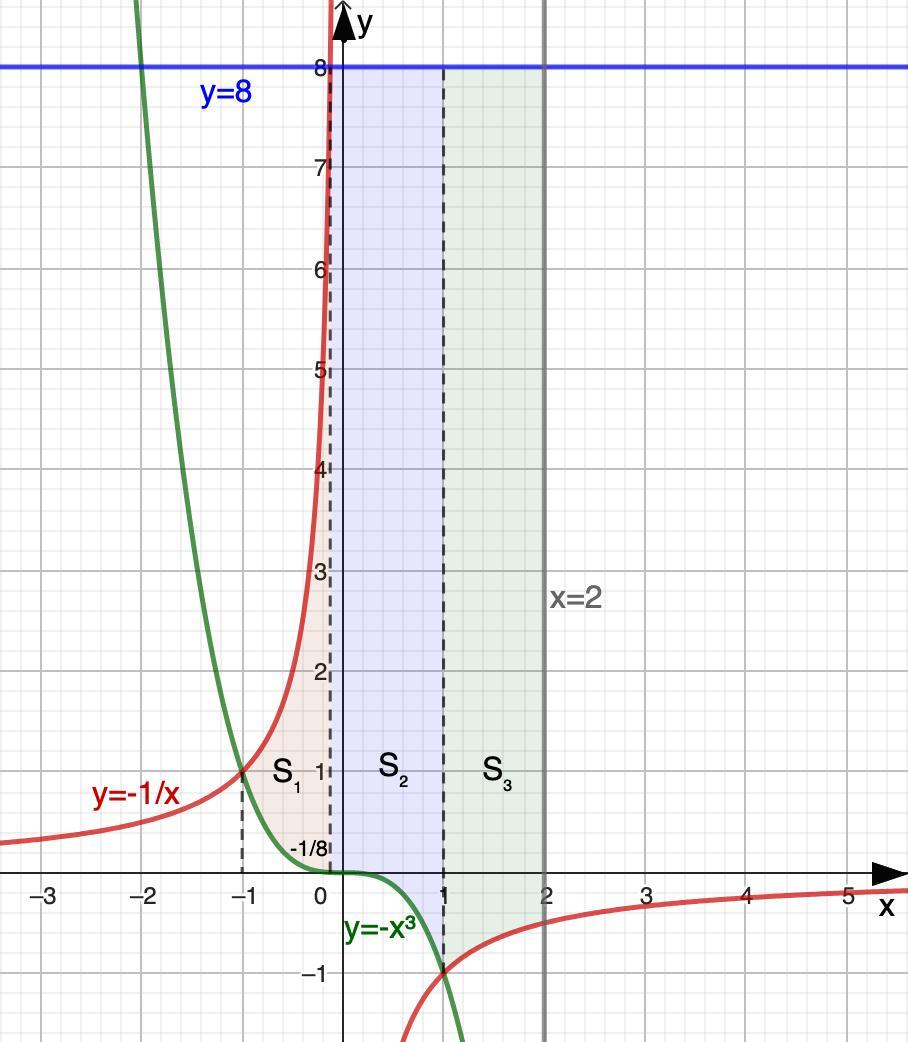
2) у=–х3, у=–1/х, у=8, х=2
Ответы
Ответ:
1) Площадь фигуры равна ед².
2) Площадь фигуры равна ед².
Пошаговое объяснение:
Найти площадь фигуры, которая ограничена линиями.
- Формула:
- Формула Ньютона - Лейбница:
1) y = -2x, y = √x, y = 2
Найдем абсциссы точек пересечения данных графиков.
y = -2x - линейная функция, график прямая,
y = √x - функция квадратного корня, график - ветвь параболы,
y = 2 - прямая, параллельная оси Ох.
y = -2x и y = √x:
-2х = √х ⇒ х = 0
y = -2x и у = 2
-2х = 2 ⇒ х = -1
y = √x и у = 2
√х = 2 ⇒ х = 4
Искомая площадь состоит из двух площадей, ограниченными снизу разными линиями:
S₁: f₂(x) = 2; f₁(x) = -2x; a = -1; b = 0
S₂: f₂(x) = 2; f₁(x) = √x; a = 0; b = 4
S = S₁ + S₂
Площадь фигуры равна ед².
2. у = -х³, у = -1/х, у = 8, х = 2
у = -х³ - кубическая парабола, расположенная во 2 и 4 четвертях,
у = -1/х - гипербола, расположенная во 2 и 4 четвертях,
у = 8 - прямая, параллельная оси Ох,
х = 2 - прямая, параллельная оси Оу.
Здесь искомая площадь разделится на три площади.
Абсциссы точек пересечения графиков:
у = -х³ и у = -1/х
⇒ x = ±1
y = -1/x и у = 8
-1/х = 8 ⇒ х = -1/8
S₁: f₂(x) = -1/х; f₁(x) = -x³; a = -1; b = -1/8
S₂: f₂(x) = 8; f₁(x) = -х³; a = -1/8; b = 1
S₃: f₂(x) = 8; f₁(x) = -1/x; a = 1; b = 2
S = S₁ + S₂ + S₃
Площадь фигуры равна ед².
#SPJ1