Предмет: Геометрия,
автор: diaaana1107
Помогите с геометрией
Приложения:
Ответы
Автор ответа:
0
Ответ:
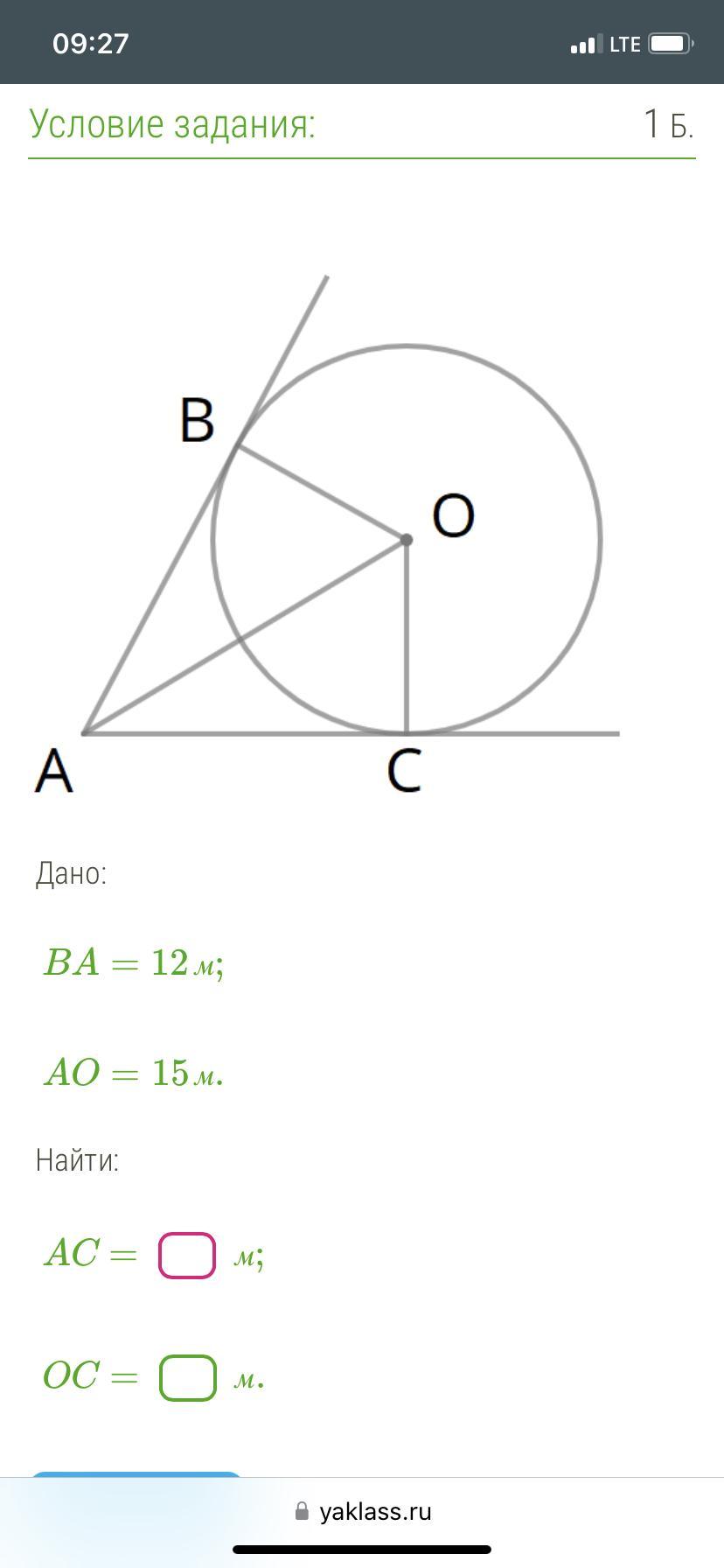
АС=12м
ОС=9 м
Решение:
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Так как АВ и ОС- касательные к оружности, то по свойству касательной, проведённой из одной точки ∠АВО=∠АСО=90°,
АС=АВ=12 м.
ΔАСО- прямоугольный. Согласно теореме Пифагора
АО²=ОС²+АС²;
15²=0С²+12²
ОС²=15²-12²=(15-12)(15+12)=3*27=3*3*9=9²(м²)
ОС=9 м
Похожие вопросы
Предмет: Русский язык,
автор: aydanabaymuhamed
Предмет: Математика,
автор: muradmmmdyarov
Предмет: Математика,
автор: serdarhumbetov61
Предмет: Математика,
автор: 09az0909das
Предмет: Математика,
автор: Аноним