Question

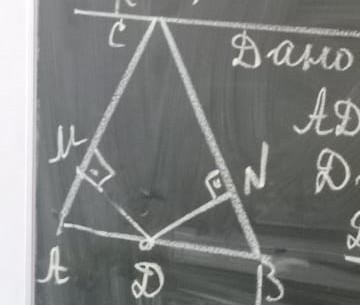
дано: AC=BC AD= DB <M=<N=90° Доказать DM=DN ​

Answer 1

Дано: треугольник ABC, в котором AC=BC, точки D и M лежат на отрезке AB, причем AD= DB, угол <M= углу <N=90°.

Чтобы доказать, что DM=DN, нужно воспользоваться теоремой Пифагора для треугольников ADM и BDN.

Для треугольника ADM:

AM^2 + AD^2 = DM^2 (теорема Пифагора)

AM^2 + DB^2 = DN^2 (теорема Пифагора для треугольника BDN)

Так как AD=DB, то AM=BM. Подставим это в первое уравнение:

BM^2 + AD^2 = DM^2

Из второго уравнения следует, что BM^2 + DB^2 = DN^2. Так как BM=AM, то можем заменить BM^2 на AM^2 во втором уравнении:

AM^2 + DB^2 = DN^2

Сравнивая это уравнение с первым, получаем, что DM=DN. Таким образом, мы доказали, что DM=DN.