Помогите пожалуйста решить 6.1 и 6 2
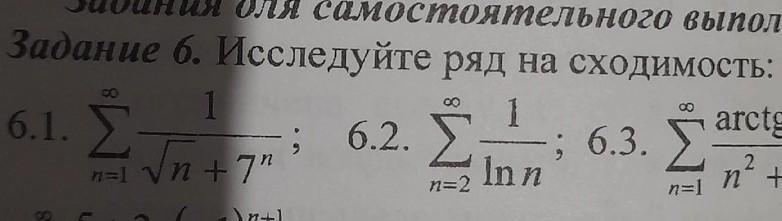
Ответы
Ответ:
Сходится; расходится.
Объяснение:
6.1. Поскольку ряд
сходится (ведь это же бесконечная убывающая геометрическая прогрессия (кто это забыл, можете применить признак Даламбера или радикальный признак Коши)), ряд
также сходится по признаку сравнения для положительных рядов.
6.2. Поскольку ряд
расходится (ведь это же знаменитый гармонический ряд (кто это забыл, примените интегральный признак Коши)), ряд
также расходится по признаку сравнения для положительных рядов.
Если Вы сомневаетесь в неравенстве можно поступить так: докажем, что
при x>1. Для этого рассмотрим функцию
Имеем: f(1)=ln 1-1=0-1=-1<0;
при x>1, поэтому функция убывает. А раз при x=1 она отрицательна, то и справа от 1 она будет отрицательной. Итак, доказано, что ln x<x при x>1, а поскольку обе функции положительны, справедливо неравенство