помогите пожалуйста решить. в первом задании Нада найти тангенс и косинус во 2 упростить
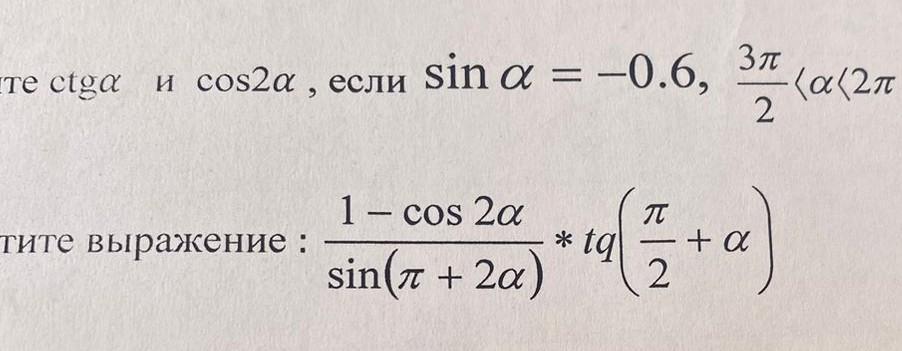
Ответы
Ответ: -0,8 / tg²a
Задание 1:
Пошаговое объяснение:Для того, чтобы решить эту задачу, нужно найти cos a, если sin a = -0.6 и π ≤ a ≤ 3π/2:
1) Найдем косинус по формуле: sin2a + cos2a = 1, отсюда cos a = √(1 – sin2a) = √(1 – 0,36) = ±0,8.
2) Но так как на промежутке (π; 3π/2) косинус отрицательный, то: cos a = -0,8
Задание 2:
1-cos2a/ sin (п+2а) × tg (п/2+а) = tg² a;
Сосчитаем каждую часть:;
1) sin (π +2а) = sin π * cos2a + cos π *sin2a = - sin2a;
sin π = 0, cos π = -1, ctg π/2 = 0;
2) tg (π/2+а) = 1 /ctg (π/2 +a) = 1/(-1/ctg a) = - ctg a;
ctg (π/2 + a) = (ctg π/2 * ctg a -1)/ (ctg a + ctg π/2) = -1/ctg a (подставим выше.);
3) 1-cos2a = 1- (1 - 2 sin²a) = 1 - 1 + 2 sin²a = 2 sin²a;
В итоге:
1-cos2a/ sin (π+2а) × tg (π/2+а) = 2 sin²a / (- sin2a * - ctg a) = 2 sin²a/ ( 2sin a * cos a * cos a/sin a) = 2 sin²a / 2 cos²a = tg² a