Question

[100 б] Обчислити площу поверхні, утвореної обертанням дуги кривої, навколо осі Ox:

Answer 1

Ответ:

Площадь поверхности вращения , образованной вращением дуги кривой около оси ОХ, заданной в параметрическом виде :

$\displaystyle \bf S_{pov.vr.}=2\pi \int\limits_{t_1}^{t_2}\, y(t)\cdot \sqrt{(x'(t))^2+(y'(t))^2}\, dt$

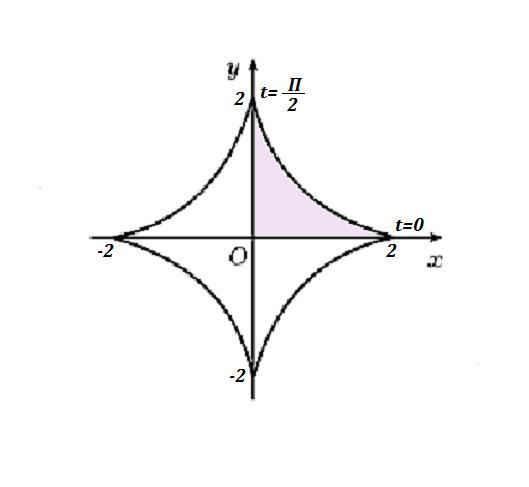
Задана астроида   $\bf \{\ x(t)=2cos^3t\ ;\ y(t)=2sin^3t\ \}$  . Это симметричная фигура относительно осей ОХ и ОУ .

Найдём производные .

$\bf x'(t)=-6cos^2t\cdot sint\ \ ,\ \ \ y'(t)=6sin^2t\cdot cost\\\\(x')^2+(y')^2=36\, cos^4t\cdot sin^2t+36\, sin^4t\cdot cos^2t=\\\\=36\, sin^2t\cdot cos^2t\, (sin^2t+cos^2t)=36\, sin^2t\cdot cos^2t=(6\, sint\cdot cost)^2$

 

$\bf y(t)\cdot \sqrt{(x')^2+(y')^2}=2\, sin^3t\cdot 6\, sint\cdot cost=12\cdot sin^4t\cdot cost$  

 

$\bf \displaystyle S=2\cdot 2\pi \int\limits_0^{\frac{\pi}{2}}\, 12\cdot sin^4t\cdot \underbrace {\bf cost\ dt}_{d(sint)}=48\pi \cdot \Big(\frac{sin^5t}{5}\Big)\Big|_{0}^{\frac{\pi }{2}}}=48\pi \Big(\frac{1}{5}-0\Big)=\frac{48\pi }{5}$