Предмет: Математика,
автор: r0m1mPL
[100 б] Обчислити площу фігури, обмежену кривими:
Приложения:
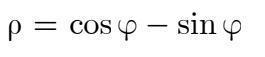
Alnadya:
0,64pi
Ответы
Автор ответа:
2
Ответ:
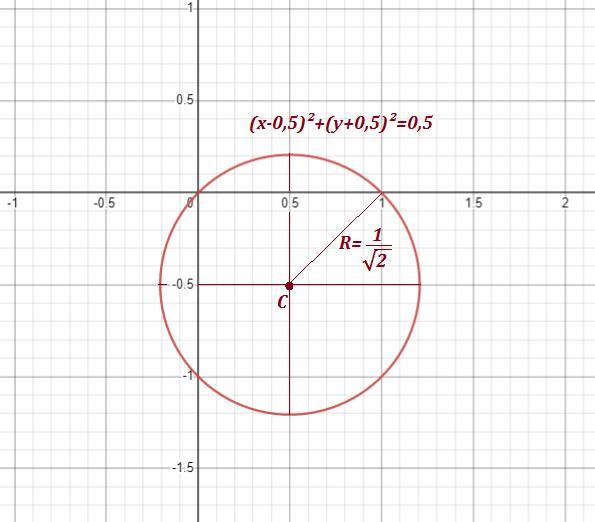
Фигура ограничена линией .
Это окружность с центром в точке ( 0,5 ; -0,5 ) и радиусом R=1/√2 , то есть уравнение в декартовых координатах выглядит так :
Так как чертить в полярной системе координат кривую долго и много надо провести вычислений, переведём уравнение из полярной системы координат в декартовую . Формулы перехода:
Подставим в заданное уравнение необходимые выражения :
Площадь фигуры, ограниченной такой кривой (окружностью) - это площадь круга с радиусом . Она равна
Можно вычислить площадь круга по формуле площади криволинейного сектора в полярной системе координат:
Приложения:
Дуууже дякую, виручили!
Можливо ще з цим допоможете `https://znanija.com/task/52185711`?)) Буду вдячний
Можливо ще з цим допоможете `https://znanija.com/task/52185711`?)) Буду вдячний
Похожие вопросы
Предмет: Биология,
автор: romanovkola232
Предмет: Химия,
автор: nastya24urban
Предмет: Українська література,
автор: ilonabenderska18
Предмет: Музыка,
автор: dmitrenkadanya458
Предмет: Русский язык,
автор: Keshij