Question

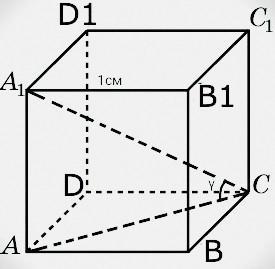
Дано куб ABCDA1B1C1D1, ребро якого дорівнює 1 см. Знайдіть синус кута γ між прямою А1С і площиною грані ABCD.

Answer 1

Ответ:

sinγ = √3/3

Объяснение:

Дано:

АВСDA₁B₁C₁D₁ - куб

А₁В₁ = 1см

∠(А₁С;(АВСD)) = γ

Найти:

sinγ

Решение:

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.

Боковые ребра куба перпендикулярны основаниям , ⇒А₁А⟂(АВСD) , значит , АС - проекция наклонной А₁С на плоскость основания , тогда, ∠А₁СА - искомый угол γ.

Повторение:

Куб - это многогранник , у которого все ребра равны и все грани состоят из квадратов.

Раз А₁С ещё и диагональ куба , то найдем его по формуле d = a√3 , где а - ребро куба.

d = 1∙√3 = √3 (см).

Рассмотрим прямоугольный △А₁АС

Синус острого угла в прямоугольном треугольнике - это отношение противолежащего катета к гипотенузе.

sinγ = A₁A/A₁C = 1/√3 = √3/3

#SPJ1