Предмет: Алгебра,
автор: LIMBAB
СРОЧНО!! 1 тригонометрическое уравнение
Приложения:
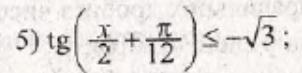
Ответы
Автор ответа:
2
Ответ:
х∈(-7π/6+2πk;-5π/6+2πk],k∈Z
Объяснение:
Вспомним правило:
tgx≤a , где а∈R
То :
-π/2 + πk < x ≤ arctga + πk , где к∈Z
Решаем наше неравенство по такому принципу:
Следовательно , х∈(-7π/6+2πk;-5π/6+2πk],k∈Z
#SPJ1
Похожие вопросы
Предмет: Українська література,
автор: romancovakira70
Предмет: Биология,
автор: juliagimla7
Предмет: Алгебра,
автор: merqum000
Предмет: Окружающий мир,
автор: gbtho
Предмет: Астрономия,
автор: osmakova03