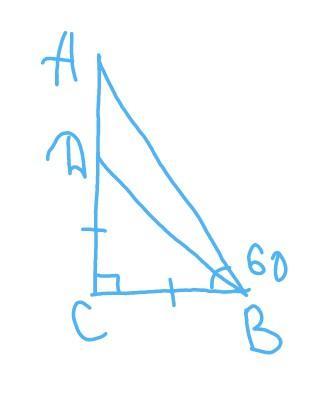
У трикутнику ABC кут С дорівнює 90°, а кут В дорівнює 60°. На катеті АС
відкладено відрізок CD рівний СВ. Знайдіть кути трикутника ABD.
Ответы
Відповідь:
Позначимо кут ABD як α, а кут ADB як β.
Оскільки СВ = CD, то трикутник BCD є рівнобедреним з кутом при вершині С в 60° (оскільки у трикутнику ABC кут В дорівнює 60°). Отже, кути BDC і BCD дорівнюють один одному і обидва дорівнюють (180°-60°)/2 = 60°.
У трикутнику ABD сума кутів дорівнює 180°, тому:
α + β + кут BAC = 180°
Але кут BAC дорівнює 90° + 60° = 150° (оскільки у трикутнику ABC кут С дорівнює 90°), тому:
α + β + 150° = 180°
або
α + β = 30°
Позначимо кут DAB як γ. Оскільки у трикутнику ABD сума кутів дорівнює 180°, то:
α + β + γ = 180°
Але знаємо, що α + β = 30°, тому:
γ = 180° - (α + β) = 180° - 30° = 150°
Отже, кути трикутника ABD дорівнюють α = 15°, β = 15° і γ = 150°.
Пояснення:
Объяснение:
∆АВС - прямоугольный:
Сумма острых углов в прямоугольном тр-ке равна 90°:
∠А=90-∠В=90-60=30°.
∆DCB - прямоугольный, равнобедреный,т.к
СD=CB .
∠CDB=∠CBD=90/2=45°.
∠АВD=∠B-∠CBD=60-45=15°
∠АDB=180-∠CDB=180-45=135° - как смежные.