Предмет: Алгебра,
автор: veronikamila65
исследовать положительный ряд на сходимость
Приложения:
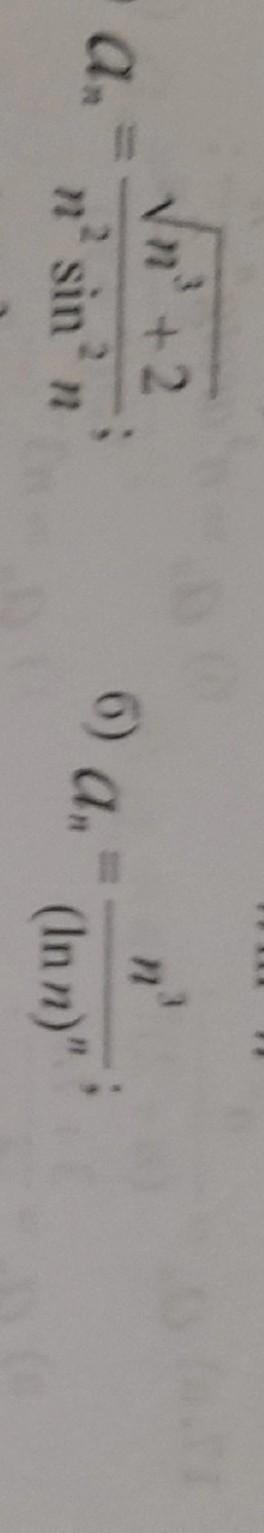
Ответы
Автор ответа:
1
Ответ:
Объяснение:
1) Заметим, во-первых, что знаменатель не обращается в ноль ни при каких n - ведь если
то
а тогда
что противоречит иррациональности числа
Имеем:
Ряд расходится (это всем известный гармонический ряд), поэтому исходный ряд также расходится по признаку сравнения.
2) Обращаю внимание на то, что суммировать нужно не с n=1, а с n=2, чтобы знаменатель не обращался в ноль.
Воспользуемся радикальным признаком Коши:
ряд сходится.
Для доказательства того, что числитель стремится к 1, можно применить правило Лопиталя:
veronikamila65:
спасибо большое
Похожие вопросы
Предмет: Математика,
автор: andrijpalijcuk75
Предмет: Математика,
автор: kamillavovchenko
Предмет: Информатика,
автор: milanatop345
Предмет: Математика,
автор: bokij79mailru