Предмет: Алгебра,
автор: iwannatouchy
Помогите пожалуйста решить системы. В первом должен получиться ответ: (6;2);(-3 1/3;-7 1/3). А во втором: [1/7;2)
Приложения:
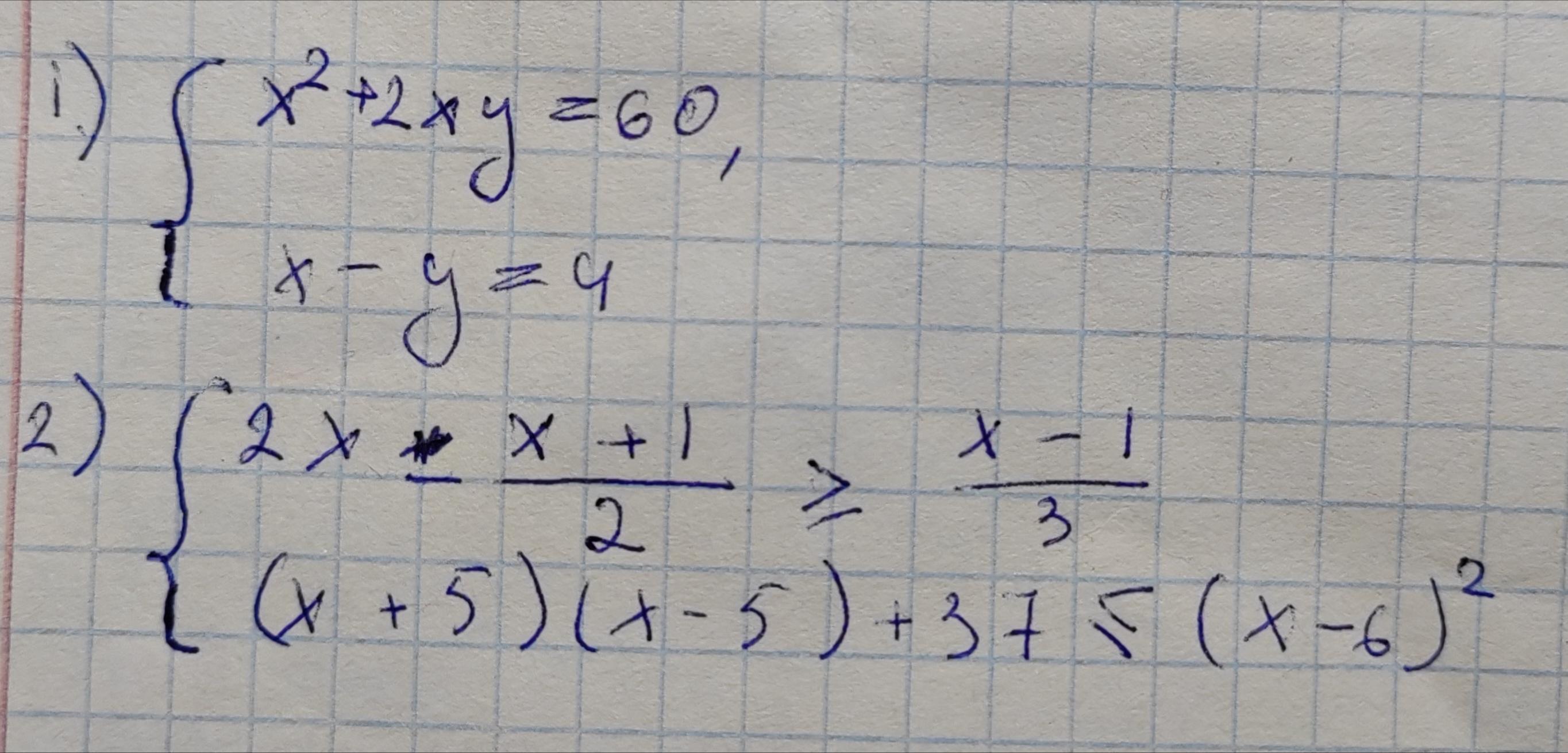
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: dasabraznak
Предмет: Геометрия,
автор: danielka25042011
Предмет: Алгебра,
автор: shudabaev122
Предмет: Українська мова,
автор: derikonnazar