Предмет: Алгебра,
автор: Tangerinee
У геометричній прогресії (bn) b1∙b3∙b11 =8. Знайдіть b2∙b8.
Приложения:
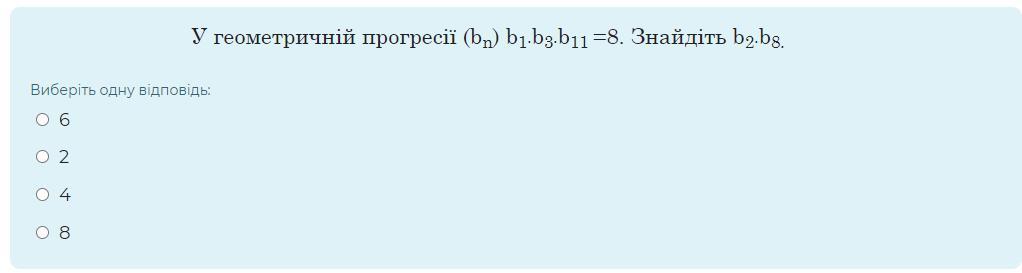
Ответы
Автор ответа:
2
Ответ:
Геометрическая прогрессия.
Формула общегo члена геометрической прогрессии : .
Похожие вопросы
Предмет: Математика,
автор: vvv078439
Предмет: История,
автор: densdevocki
Предмет: Математика,
автор: maria9076886
Предмет: Математика,
автор: sophiastar0610