Предмет: Математика,
автор: smartfish228
Даю 100 баллов , решить и расписать по минимуму (спамеры мимо)
Приложения:

Ответы
Автор ответа:
1
Ответ:
Б)
А)
Пошаговое объяснение:
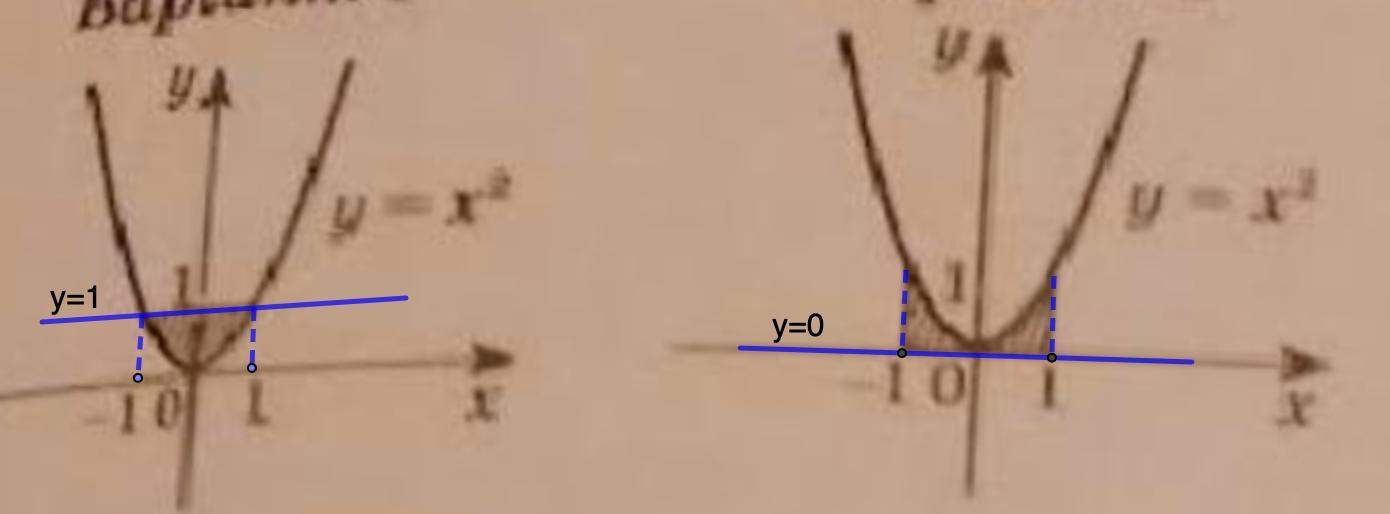
Какое из приведенных ниже выражений равно площади заштрихованной на рисунке фигуры?
- Площадь фигуры, отграниченной линиями равна:
x = b - ограничение справа;
х = а - ограничение слева;
f₂(x) - ограничение сверху;
f₁(x) - ограничение снизу.
1) Рисунок 1.
Справа функция ограничена х = 1 ⇒ b = 1;
Слева: х = -1 ⇒ a = -1;
Сверху: y = 1 ⇒ f₂(x) = 1;
Снизу: у = х² ⇒ f₁(x) = x²
Подставим значения в формулу:
Ответ: Б)
2) Рассмотрим второй рисунок.
Справа функция ограничена х = 1 ⇒ b = 1;
Слева: х = -1 ⇒ a = -1;
Сверху: y = х² ⇒ f₂(x) = х²;
Снизу: у = 0 ⇒ f₁(x) = 0.
Подставим значения в формулу:
Ответ: А)
Приложения:
natalyabryukhova:
рада
допоможіть мені будь ласочка з завданням в моєму профілі, будь ласка дуже потрібно
Похожие вопросы
Предмет: Математика,
автор: ajnuraisamedinova
Предмет: Математика,
автор: Bodya21108
Предмет: Французский язык,
автор: steblinaalina883
Предмет: Литература,
автор: Spies