Question

ПОМОГИТЕ ПОЖАЛУЙСТА, ОЧЕНЬ СРОЧНО
В правильной четырехугольной пирамиде плоский угол наверху - α. Находить
Площадь боковой поверхности конуса, описанная вокруг пирамиды, если ее высота равна H.

Answer 1

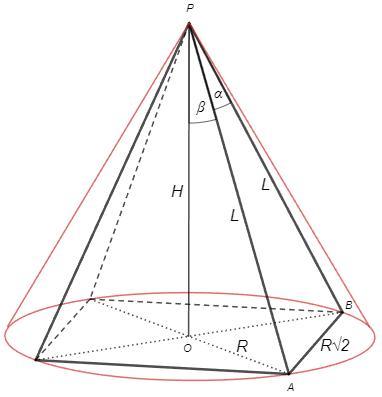
Правильная пирамида - боковые ребра равны, вершина падает в центр основания. Конус описан около пирамиды - основание конуса описано около основания пирамиды. Радиус конуса R - радиус описанной окружности квадрата, половина диагонали. Тогда сторона квадрата R√2. Образующая конуса L - боковое ребро пирамиды.

∠APB=a, ∠APO=b

△APB (р/б, т косинусов):

2R^2 =2L^2 (1-cosa) => (R/L)^2 =1-cosa

△APO:  R/L =sinb

=> sinb^2 =1-cosa

=> cosb^2 =cosa

L =H/cosb =H/√cosa

R =L sinb =H/√cosa *√(1-cosa)

Sбпк =пRL =п H^2 √(1-cosa)/cosa