Question

Помогите пожалуйстаа, 4 задание

Answer 1

Ответ:

Косинус угла между диагональю боковой грани и другой боковой гранью призмы равен 0,54.

Объяснение:

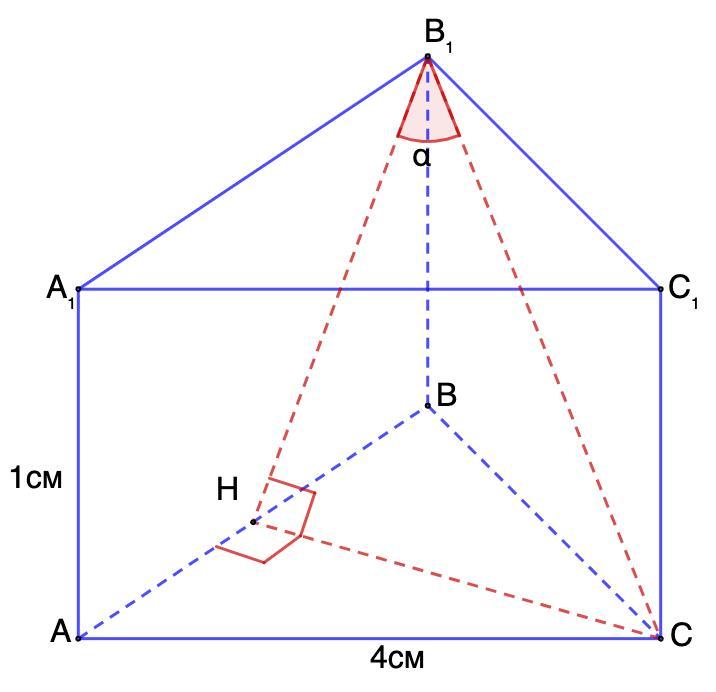
4. Длина ребра основания правильной треугольной призмы равна 4 см, а ее высота - 1 см. Найдите косинус угла между диагональю боковой грани и другой боковой гранью призмы.

Дано: АВСА₁В₁С₁ - правильная треугольная призма;

АВ = 4 см; АА₁ = 1 см;

В₁С - диагональ;

Найти: косинус угла между В₁С и (АВ₁В).

Решение:

• В правильной треугольной призме основания - равносторонние треугольники, а боковые грани - равные прямоугольники.

Определимся с углом.

• Углом между прямой и плоскостью называют угол между прямой и ее проекцией на эту плоскость.

Из точки опустим перпендикуляр СН на плоскость (АВ₁В).

В₁Н - проекция В₁С на плоскость   (АВ₁В).

⇒ ∠НВ₁С - искомый угол.

Обозначим этот угол α.

• Косинус угла - отношение прилежащего катета к гипотенузе.

$\displaystyle cos\;\alpha =\frac{B_1H}{B_1C}$

Найдем В₁С.

Рассмотрим ΔВ₁ВС - прямоугольный.

По теореме Пифагора найдем В₁С:

В₁С² = ВВ₁² + ВС² = 1 + 16 = 17   ⇒ В₁С = √17 (см)

Найдем В₁Н.

Рассмотрим ΔНВ₁В - прямоугольный.

СН - высота ΔАВС - равностороннего.

• В равностороннем треугольнике высоты являются медианами.

⇒ АН = НВ = 4 : 2 = 2 (см)

По теореме Пифагора найдем В₁Н:

В₁Н² = В₁В² + НВ² = 1 + 4 = 5  ⇒ В₁Н = √5 (см).

$\displaystyle \bf cos\;\alpha =\frac{\sqrt{5} }{\sqrt{17} } =\sqrt{\frac{5}{17} } \approx 0,54$

#SPJ1