3.Упростить выражение:
а) sin2a/ 2tga
б) 1+соs 2a/1-cos2a
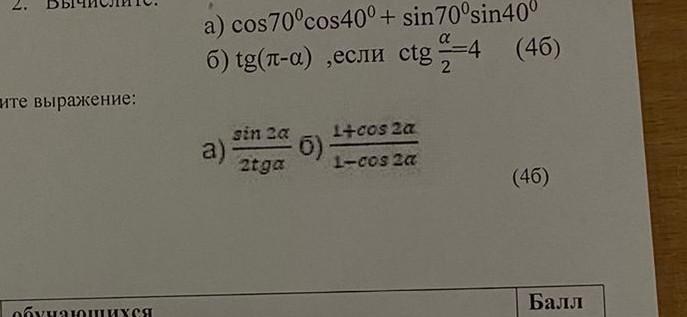
Ответы
Ответ:
Объяснение:
А)
Перепишем тангенс через синус и косинус:
tg a = sin a / cos a
Тогда:
sin 2a / 2tg a = sin 2a / (2sin a / cos a) = (sin 2a * cos a) / (2sin a) = cos a / 2
Таким образом, выражение sin 2a / 2tg a упрощается до cos a / 2.
B)
Мы можем воспользоваться формулой сокращения для тригонометрического выражения:
cos 2a = cos² a - sin² a
Тогда:
1 + cos 2a = 1 + cos² a - sin² a
(1 - cos 2a)(1 + cos 2a) = (1 - cos² 2a) = sin² 2a
Таким образом, исходное выражение принимает вид:
(1 + cos 2a) / (1 - cos 2a) = [(1 + cos² a - sin² a) / (2 cos² a)] / [(cos² a - sin² a) / (2 cos² a)] = (1 + cos² a - sin² a) / (cos² a - sin² a) = [(1 + cos² a) - sin² a] / [(1 - sin a)(1 + sin a)] = [(1 + cos a)(1 - cos a)] / [(1 - sin a)(1 + sin a)] = (1 - cos a) / (1 + sin a)
Таким образом, выражение 1 + cos 2a / 1 - cos 2a упрощается до (1 - cos a) / (1 + sin a).
Объяснение:
a)
б)