Предмет: Алгебра,
автор: SaiHariK
35.23 найдите наименьшее целое число, являющееся решением неравенства:
Приложения:

Ответы
Автор ответа:
2
1)
Ответ:
Наименьшее целое число, которое является решением неравенства:
2)
Ответ: Ответ:
Наименьшее целое число, которое является решением неравенства:
3)
Ответ:
Наименьшее целое число, которое является решением неравенства:
4)
Ответ:
Нет наименьшего целого числа, которое является решением неравенства
Приложения:
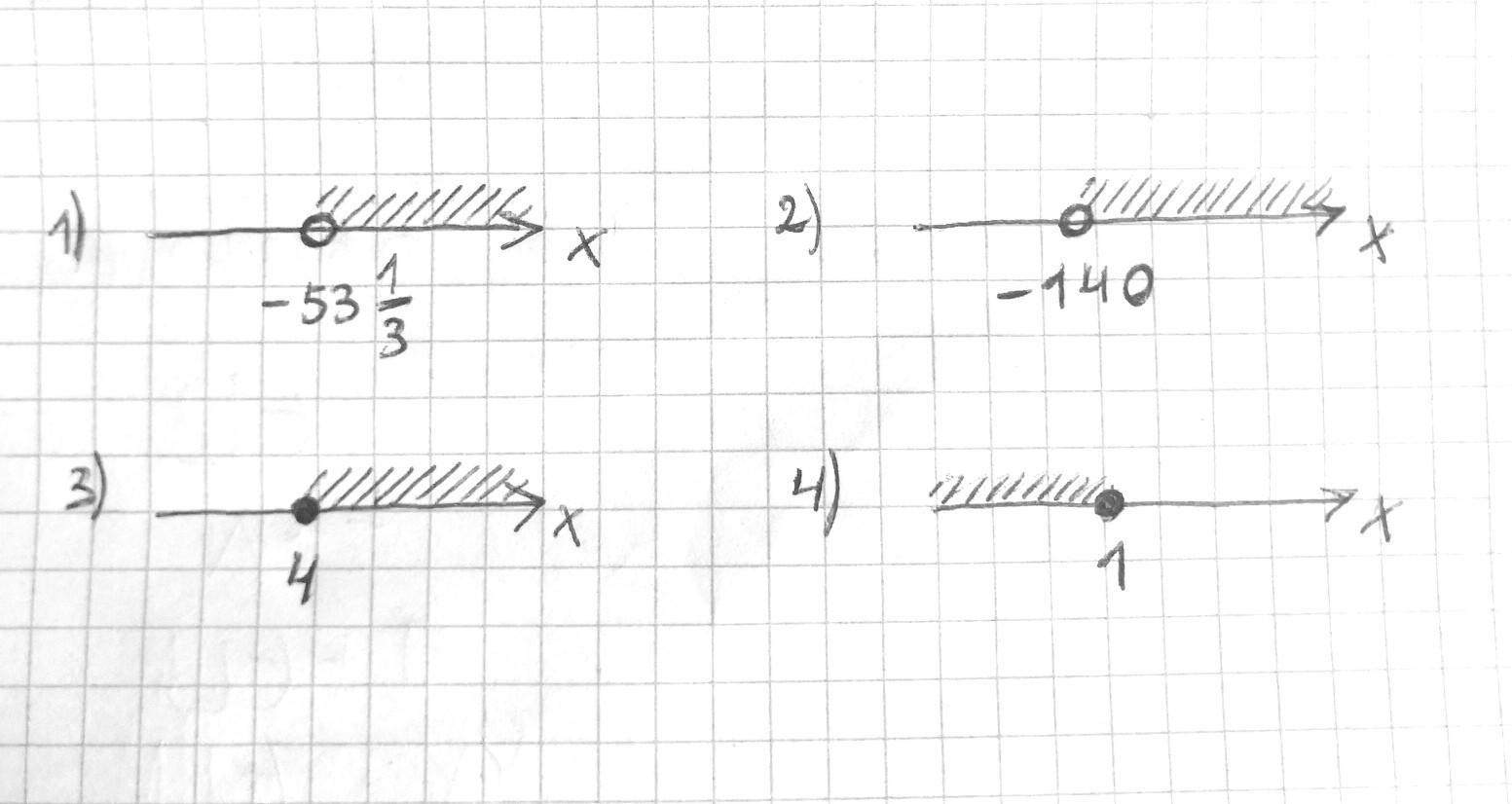
Похожие вопросы
Предмет: Русский язык,
автор: asikaskaasiasya
Предмет: Математика,
автор: sashadgordon2010
Предмет: Геометрия,
автор: koval6432
Предмет: Биология,
автор: mimimizka111
Предмет: Английский язык,
автор: sokol2007dariy