Предмет: Алгебра,
автор: binka0909
помогите пожалуйста " 3
Приложения:
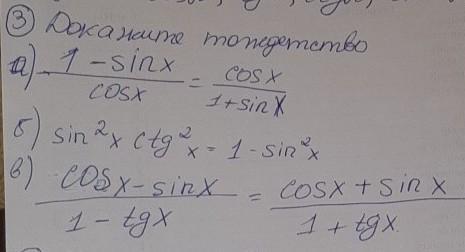
Ответы
Автор ответа:
0
Объяснение:
№3 докажите тождество:
перемножим крест на крест:
(1–sinx)(1+sinx)=cosx•cosx
1–sin²x=cos²x
cos²x=cos²x
Доказано.
В решении использована формула:
sin²x+cos²x=1 → 1–sin²x=cosx
б)
в доказательстве использованы формулы
в)
(соsx–sinx)(1+tgx)=(cosx+sinx)(1–tgx)
преобразуем левую часть:
теперь преобразуем правую часть:
(cosx+sinx)(1–tgx)
левая часть равна правой:
Доказано.
В доказательстве использованы формулa:
Похожие вопросы
Предмет: Английский язык,
автор: alnuri30102010
Предмет: Биология,
автор: ulabutenko40
Предмет: Математика,
автор: bekarystanovaalfia30
Предмет: Геометрия,
автор: VladNotLazy27567
Предмет: Математика,
автор: kudratova47karina