Question

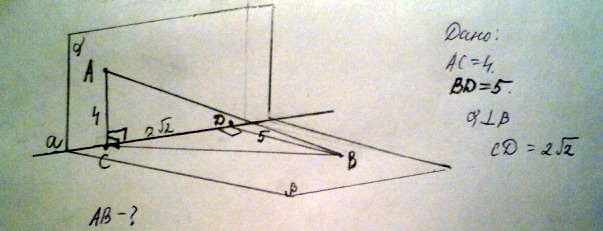
Плоскость альфа и бета перпендикулярны. Прямая альфа - линия их пересечения. В плоскости альфа взято точку A, а в плоскости бета - точку B такие, что расстояния от них до прямой альфа равны 4 см и 5 см соответственно. Найдите расстояние между точками A и B, если расстояние между их проекциями на прямую альфа равен 2 * sqrt2 см

Answer 1

Решение:

1) α ⊥ β, AC ⊥ a, BD ⊥ a;

2) Р-м прямоугольный Δ BDC:

за т. Пифагора, гипотенуза BC равна:

    $BC= \sqrt{BD^2+CD^2}=\sqrt{5^2+(2\sqrt{2})^2 } = \sqrt{25+8}=\sqrt{33} \:\: (cm)$

3)AC ∈ α, BC ∈ β, α ⊥ β  ⇒  AC ⊥ BC  ⇒  Δ ABC — прямой  ⇒

⇒  за т. Пифагора, гипотенуза AB равна:

    $AB = \sqrt{AC^2+BC^2}= \sqrt{4^2+(\sqrt{33})^2}=\sqrt{16+33}=\sqrt{49}=7 \:\: (cm)$

Ответ: Расстояние между точками A и B равно 7 см.