СРОЧНО!!! 75 баллов даю
Ответы
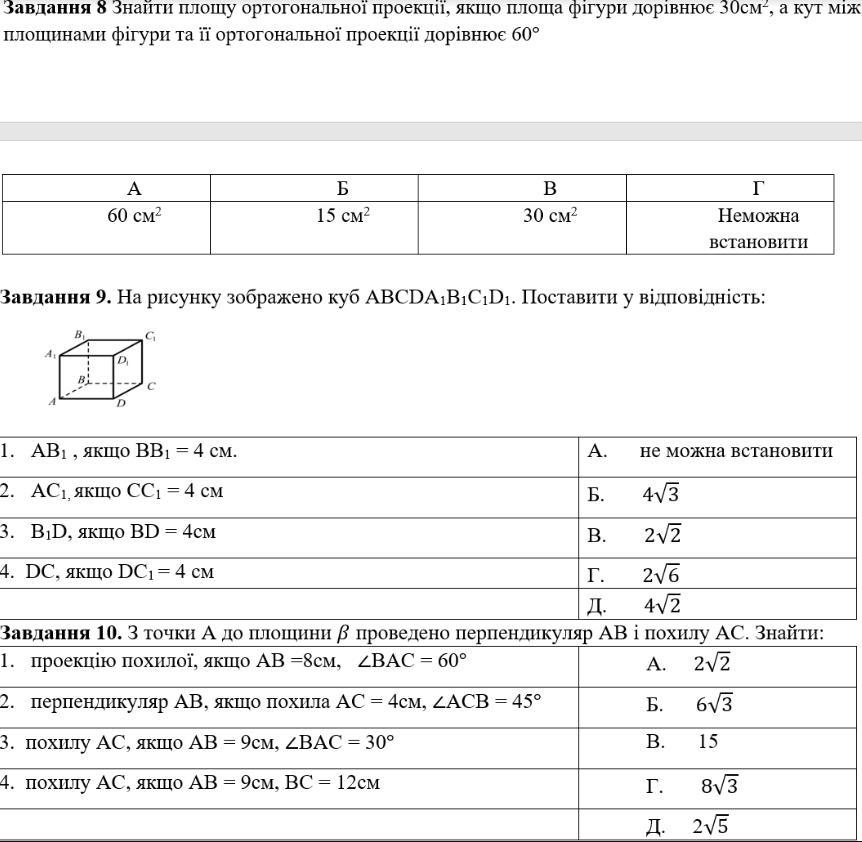
Ответ:8.Для знаходження площі ортогональної проекції потрібно використовувати формулу:
Площа ортогональної проекції = Площа фігури * cos(кут між площинами)
Відповідно до задачі, площа фігури дорівнює 30см², а кут між площинами фігури та її ортогональної проекції дорівнює 60°.
Застосуємо формулу:
Площа ортогональної проекції = 30 см² * cos(60°)
Площа ортогональної проекції = 30 см² * 0,5
Площа ортогональної проекції = 15 см²
Отже, площа ортогональної проекції дорівнює 15 квадратним сантиметрам.
9.хз
10.За теоремою Піфагора ми можемо знайти довжину похилої AC:
AC² = AB² + BC²
де BC - відрізок, проведений від точки В до точки С.
Так як ми знаємо, що <BAC = 60°, то ми можемо визначити відношення довжин сторін трикутника АВС за допомогою тригонометричних функцій:
sin 60° = BC/AC
√3/2 = BC/AC
BC = (AB·√3)/2 = (8·√3)/2 = 4√3
Тепер ми можемо обчислити довжину похилої:
AC² = AB² + BC² = 8² + (4√3)² = 64 + 48 = 112
AC = √112 = 4√7
Щоб знайти проекцію похилої на площину, ми можемо скористатися відношенням:
cos 60° = AB/AC
1/2 = AB/AC
AB = AC/2 = (4√7)/2 = 2√7
Отже, проекція похилої на площину дорівнює 2√7 см.
Объяснение:потому что так