Question

Геометрия помогите срочно

Answer 1

Ответ:

$P=\dfrac{2b}{\cos\dfrac{\alpha }{2}}$

Объяснение:

Свойства диагоналей ромба:

• диагонали ромба взаимно перпендикулярны;
• диагонали ромба точкой пересечения делятся пополам;
• диагонали ромба лежат на биссектрисах его углов.

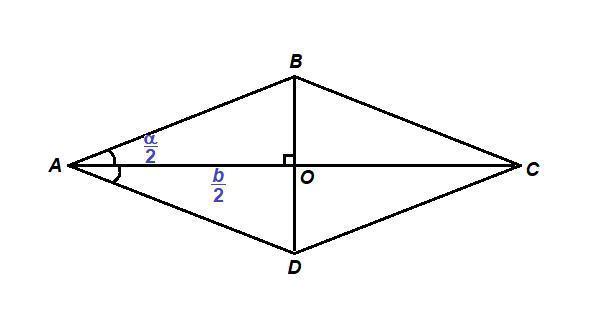
Если АС = b, то АО = 0,5 b.

∠А = α, тогда ∠ОАВ = 0,5 α

∠АОВ = 90°.

Из прямоугольного треугольника АОВ:

$\cos\angle OAB=\dfrac{AO}{AB}$

$AB = \dfrac{AO}{\cos\angle OAB}=\dfrac{b}{2}:\cos \dfrac{\alpha}{2}=\dfrac{b}{2\cos \dfrac{\alpha }{2}}$

Периметр ромба:

$P=4AB=4\cdot \dfrac{b}{2\cos\dfrac{\alpha}{2}}$

$\boldsymbol{P=\dfrac{2b}{\cos\dfrac{\alpha }{2}}}$

Answer 2

Объяснение:

диагнали ромба пересекаются под прямым углом и точкой пересечения делятся пополам.

диагнали ромба являются биссектрисами его углов:

a - cторона

соs(α/2)=(b/2)/a

а=(b/2)/cos(α/2)

P=4a=(4•(b/2))/cos(α/2)=2b/(cos(α/2))