Question

решите пожалуйста , даю 40 баллов .Висоти АК і BD гострокутного трикутника АВС перетинаються в точці Н. Відомо, що АН=ВС. Знайдіть кут ВАС.

Answer 1

Ответ:

Угол ВАС равен 45°.

Объяснение:

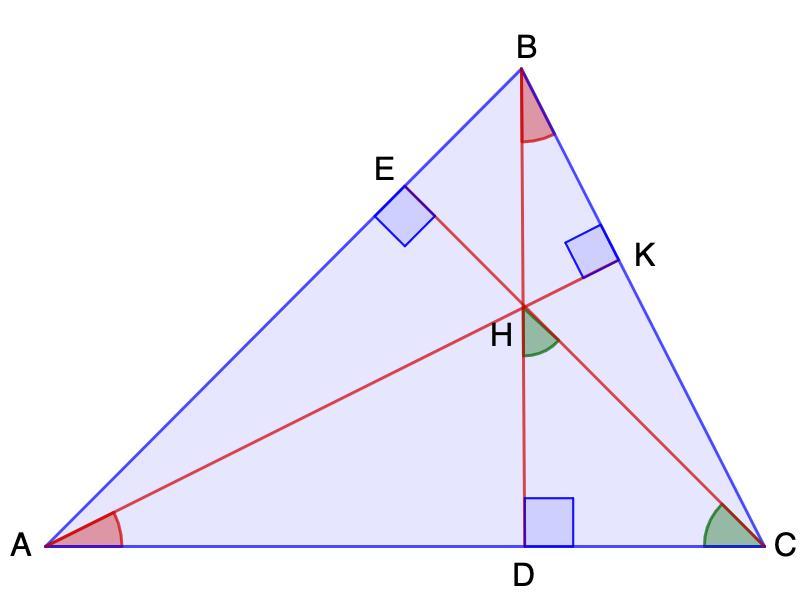
Высоты АК и BD остроугольного треугольника АВС пересекаются в точке Н. Известно, что АН = ВС. Найдите угол ВАС.

Дано: ΔАВС - остроугольный;

АК и BD - высоты;

АК ∩ BD = Н; АН = ВС.

Найти: ∠ВАС.

Решение:

• Высоты треугольника пересекаются в одной точке.

⇒ СЕ - высота.

• Сумма острых углов прямоугольного треугольника равна 90°.

ΔАКС - прямоугольный.

⇒ ∠КАС = 90° - ∠АСВ

ΔDBC - прямоугольный.

⇒ ∠DBC = 90° - ∠АСВ

• Если правые части равенства равны, то равны и левые.

⇒ ∠КАС = ∠DBC

Рассмотрим ΔАНD и ΔBCD - прямоугольные.

∠КАС = ∠DBC

АН = ВС (условие)

ΔАНD и ΔBCD (по гипотенузе и острому углу)

⇒ DH = DC (как соответственные элементы)

Рассмотрим ΔDHC - прямоугольный.

DH = DC ⇒ ΔDHC - равнобедренный.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠DHC + ∠DCH = 90°

• Углы при основании равнобедренного треугольника равны.

⇒ ∠DHC = ∠DCH = 90° : 2 = 45°

Рассмотрим ΔАЕС - прямоугольный.

∠ЕАС = 90° - ЕСА = 90° - 45° = 45° (сумма острых углов прямоугольного треугольника)

Угол ВАС равен 45°.

#SPJ1