Предмет: Геометрия,
автор: e2mwgfj9j2
найдите площадь полной поверхности куба вписанного в сферу радиусом 1
Ответы
Автор ответа:
2
Ответ:
Sполн. = 8ед²
Объяснение:
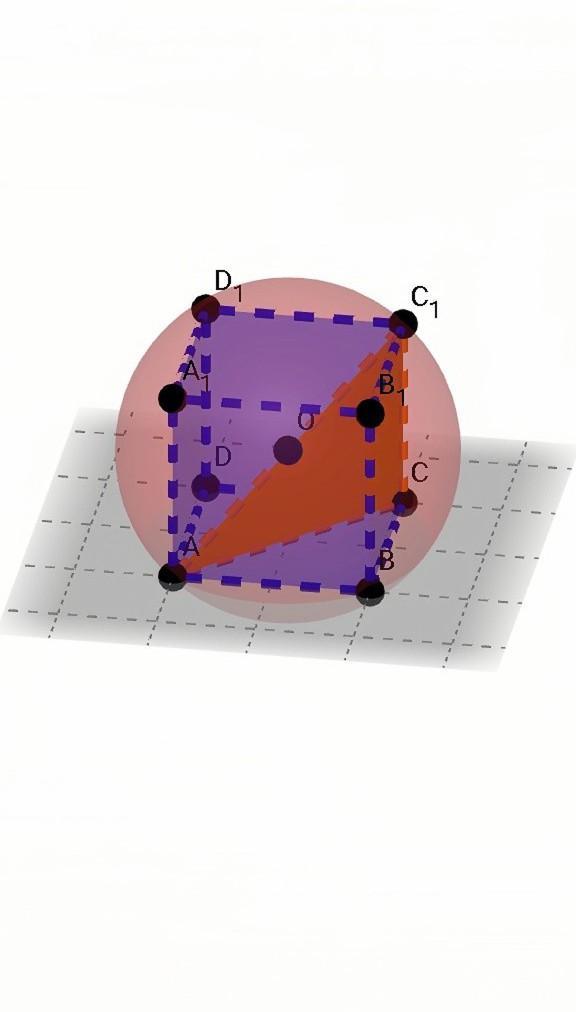
- Проведём диагональ АС₁. Она пройдет через центр сферы и будет его диаметром. ОС₁ = АО = 1ед.
- Как известно, диаметр в два раза больше самого радиуса: D = 2ед.
- Площадь полной поверхности куба равна сумме всех площадей его граней. Все грани - квадраты, их 6, следовательно формула для вычисления площади полной поверхности куба выглядит так: Sполн. = 6а², где а - ребро куба. Найдем его через известную нам диагональ. Формула диагонали куба: D = a√3. Отсюда выразим сторону:
⠀⠀⠀⠀а = D/√3
⠀⠀⠀⠀а = 2/√3ед.
- Сторону нашли, тогда площадь полной поверхности равна: Sполн. = 6 * (2/√3)² = 6 * 4/3 = 8ед²
#SPJ1
Приложения:
Похожие вопросы
Предмет: Биология,
автор: liesswaks
Предмет: Українська мова,
автор: f9ssdmbt94
Предмет: Физика,
автор: 4itornikossas
Предмет: Українська література,
автор: anjanchuk
Предмет: История,
автор: bokiy1991