Question

30 баллов!!!

Рисунок к задаче обязателен.

Answer 1

Ответ:

Длина отрезка АВ равна R√2.

Объяснение:

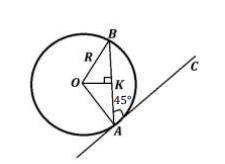
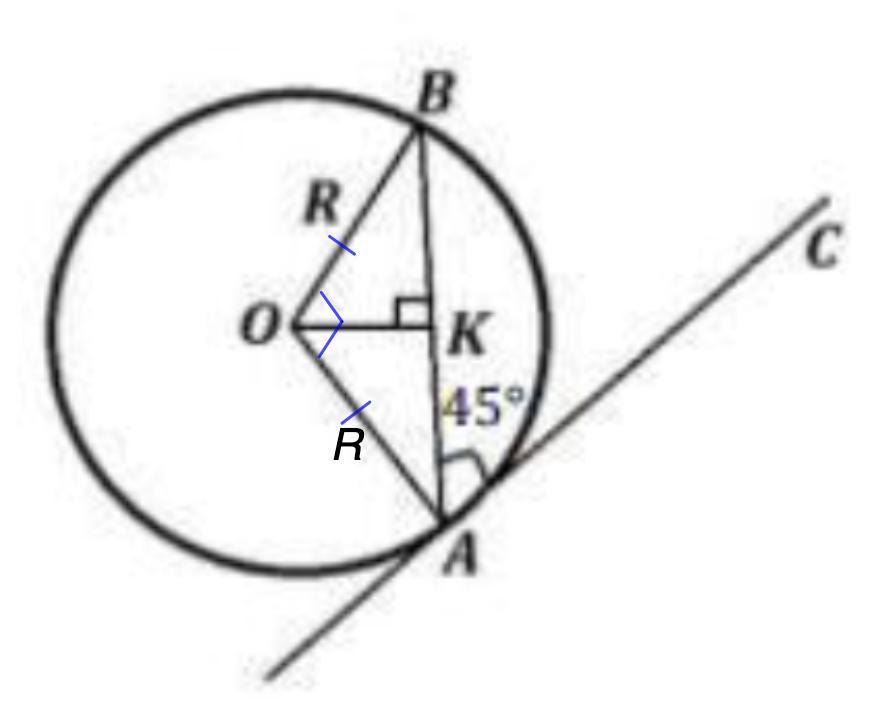
Через точку А окружности с центром в точке O радиуса R проведены касательная СА и хорда АВ, угол между которыми 45°. Найдите длину АВ (рис.1).

Дано: Окр.(О;R)

CA - касательная; АВ - хорда;

∠ВАС = 45°,

Найти: АВ

Решение:

∠ВАС = 45°

• Угол между касательной и хордой, проведенной через точку касания, равен половине градусной меры дуги, отсекаемой хордой.

⇒ ◡АВ = 45° · 2 = 90°

• Центральный угол измеряется градусной мерой дуги, на которую он опирается.

⇒ ∠АОВ = 90° (центральный)

Рассмотрим ΔАОВ - прямоугольный.

АО = ОВ = R.

⇒ ΔAOB - равнобедренный.

По теореме Пифагора найдем АВ:

АВ² = ОА² + ОВ² = R² + R² = 2R²   ⇒  AB = R√2