Question

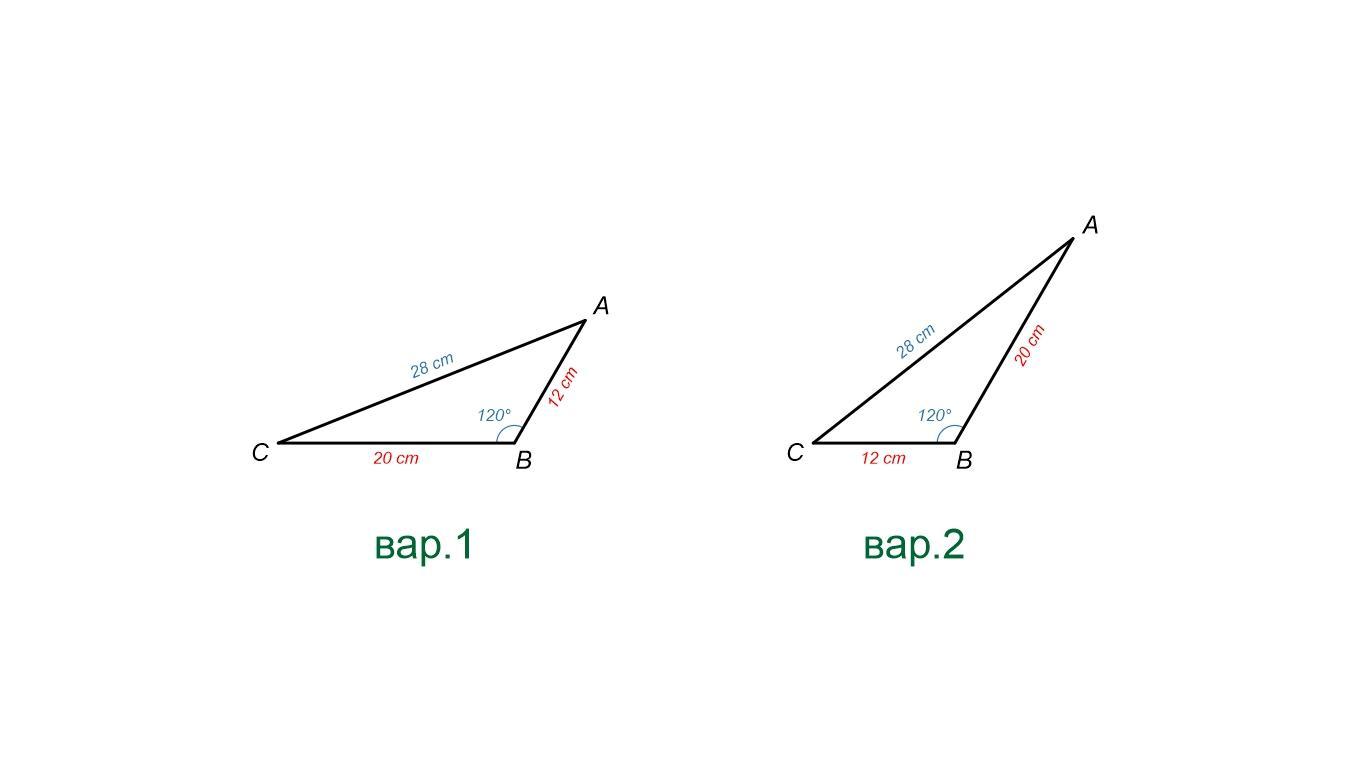
обчисліть сторони трикутника, якщо AC=28 cм LB=120 AB+BC=32см​

Answer 1

Решение:

AB + BC = 32

⇒ AB = 32 - BC

Далее используем Теорему Косинусов: квадрат стороны треугольника равен сумме квадратов двух других его сторон, минус удвоенное произведение этих сторон на косинус угла между ними.

AC² = AB² + BC² - 2·AB·BC·cos(∠B)

28² = (32-BC)² + BC² - 2·(32-BC)·BC·(-1/2)

784 = 32² - 2·32·BC + BC² + BC² + (32-BC)·BC

784 = 1024 - 64·BC + 2·BC² + 32·BC - BC²

BC² - 32·BC + 240 = 0

Решаем квадратное уравнение:

D = b² - 4ac = (-32)² - 4·1·240 = 1024 - 960 = 64

$BC_{1} = \frac{-b + \sqrt{D}}{2a} = \frac{-(-32) + \sqrt{64}}{2*1} = \frac{32+8}{2}=\frac{40}{2} = 20cm$

$BC_{2} = \frac{-b - \sqrt{D}}{2a} = \frac{-(-32) - \sqrt{64}}{2*1} = \frac{32-8}{2}=\frac{24}{2} = 12cm$

Подставляем полученные варианты значений BC в первое уравнение, и найдём варианты значений AB:

AB₁ = 32 - BC₁ = 32 - 20 = 12 cm

AB₂ = 32 - BC₂ = 32 - 12 = 20 cm

Итого, имеем 2 варианта решения задачи:

Ответ₁: AB₁ = 12 см; BC₁ = 20 см; AC = 28 см.

Ответ₂: AB₂ = 20 см; BC₂ = 12 см; AC = 28 см.