Предмет: Алгебра,
автор: vladzavadskiu
розв'яжіть нерівність 7(x-3)≤(3-x)(3+x)
Ответы
Автор ответа:
1
Ответ:
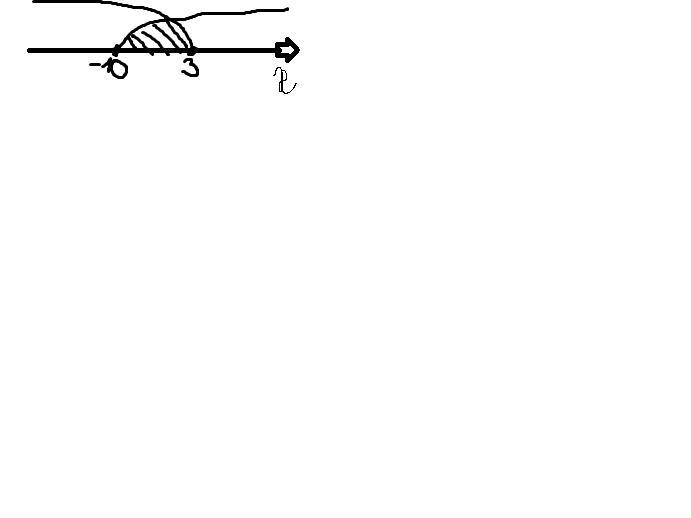
-10 ≤ x ≤ 3 або x є [-10, 3]
Объяснение:
Почнемо з розкриття правої частини нерівності:
(3-x)(3+x) = 9 - x^2
Теперь замінимо це в нерівність:
7(x-3) ≤ 9 - x^2
Розкриваємо дужки:
7x - 21 ≤ 9 - x^2
Переносимо всі члени в ліву частину:
x^2 + 7x - 30 ≤ 0
Теперь знаходимо корені цього квадратного рівняння:
x1 = -10, x2 = 3
Тож, відповідь:
-10 ≤ x ≤ 3.
Автор ответа:
1
7(x-3)<=(3-x)(3+x)
7(x-3)+(x-3)(3+x)=<0
(x-3)(7+3+x)=<0
(x-3)(10+x)=<0
{x-3=<0
{10+x=>0
{x-3>=0
{10+x=<0
{x<=3
{x=>-10
{x>=3
{x<=-10
x Є [-10; 3]
Другий випадок - ∅.
Пряма на фото
Приложения:
Похожие вопросы
Предмет: География,
автор: harkovskaaelena31
Предмет: Алгебра,
автор: babicmaksim10
Предмет: Українська мова,
автор: AlexanderGermaniuk
Предмет: Математика,
автор: queensvip
Предмет: Математика,
автор: Аноним