Предмет: Алгебра,
автор: dianaaaagggggg
тригонометричні рівняння!
2 рівняння
Приложения:
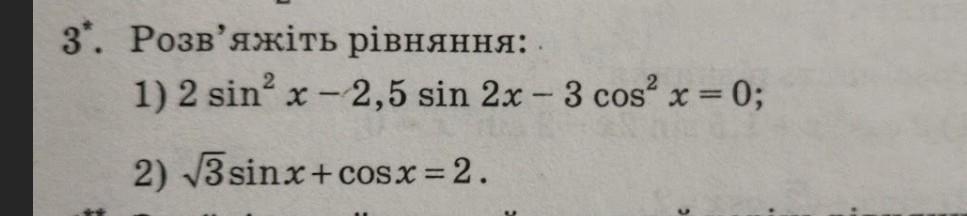
Ответы
Автор ответа:
0
Ответ:
1) Однородное тригонометрическое уравнение .
Ответ: .
Делим обе части равенства на , получим
Получили формулу синуса суммы углов .
Ответ: .
Похожие вопросы
Предмет: Алгебра,
автор: svetalisienko01
Предмет: Математика,
автор: tarasov19890212
Предмет: Математика,
автор: tekahiya
Предмет: Биология,
автор: ruslanarabich
Предмет: Математика,
автор: seredin45