Question

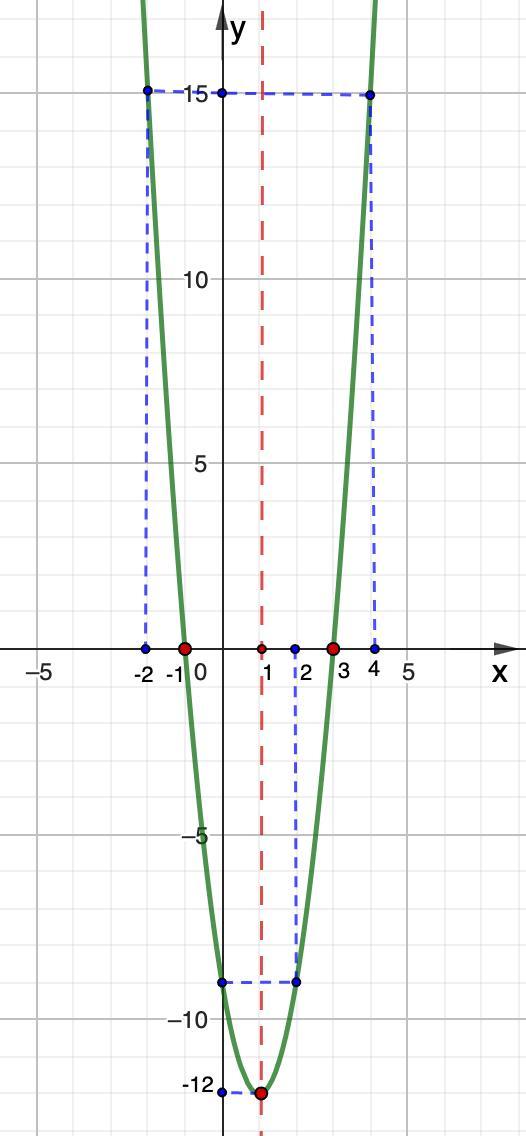
1. Дана функция y=3x²-6x-9. А) Найдите координаты вершины параболы Б) Найдите точки пересечения с осями координат. В) Найдите ось симметрии параболы. Г) Постройте график функции.​

Answer 1

Ответ:

А) Координаты вершины (1; -12)

Б) Точка пересечения с осью Оу имеет координаты (0; -9).

Точки пересечения с осью Ох имеют координаты (-1; 0) и (3; 0)

В) Уравнение оси симметрии х = 1

Объяснение:

Дана функция y=3x²-6x-9.

А) Найдите координаты вершины параболы

Б) Найдите точки пересечения с осями координат.

В) Найдите ось симметрии параболы.

Г) Постройте график функции.​

y = 3x² - 6x - 9

-квадратичная функция вида y = ax² + bx + c, график - парабола, а = 3 >0 ⇒ ветви вверх.

А) Найдем координаты вершины параболы.

$\displaystyle \bf x_0=-\frac{b}{2a}=-\frac{-6}{2\cdot 3} =1\\\\y_0=y(1)=3\cdot1-6\cdot1-9=-12$

Координаты вершины (1; -12)

Б) Найдем точки пересечения с осями.

1. С осью Оу   ⇒   х = 0

у(0) = -9

⇒ Точка пересечения с осью Оу имеет координаты (0; -9)

2. С осью Ох   ⇒   у = 0

$\displaystyle \bf 0=3x^2-6x-9\;\;\;\;\;|:3\\\\x^2-2x-3=0\\\\D=4+12=16\;\;\;\Rightarrow \;\;\;\sqrt{D}=4\\ \\x_1=\frac{2+4}{2}=3;\;\;\;\;\;x_2=\frac{2-4}{2}=-1$

Точки пересечения с осью Ох имеют координаты (-1; 0) и (3; 0)

В) Ось симметрии.

х = m, где m = x₀, то есть абсцисса вершины параболы.

⇒ Уравнение оси симметрии х = 1

Г) Построим график.

Дополнительные точки:

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c|c|c| }\cline{1-5}x& 0& 2 & -2& 4 \\\cline{1-5}y& -9 & -9 & 15& 15 \\\cline{1-5}\end{array}$

Строим график.

#SPJ1