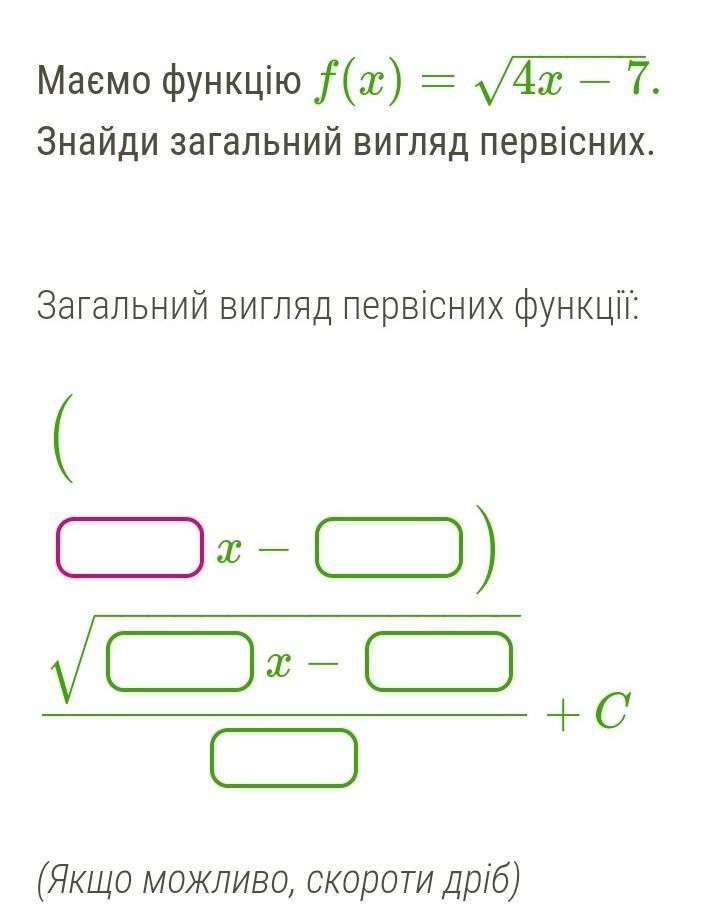
Маємо функцію f(x) = √√4x - 7. Знайди загальний вигляд первісних. Загальний вигляд первісних функції:
Ответы
Ответ:
Для того, щоб знайти загальний вигляд первісних функції f(x), ми повинні обчислити її нескінченний інтеграл. Але спочатку ми можемо спростити вираз під коренем, щоб отримати більш зручний вираз:
f(x) = √√4x - 7
= ((4x - 7)^1/2)^1/2
= (4x - 7)^(1/4)
Тепер ми можемо обчислити первісну функції f(x):
F(x) = ∫(4x - 7)^(1/4) dx
Щоб знайти цю первісну, ми можемо використовувати формулу інтегрування для степеневих функцій:
∫x^n dx = (x^(n+1))/(n+1) + C, де C - довільна константа.
Таким чином, ми отримуємо:
F(x) = ∫(4x - 7)^(1/4) dx
= (4x - 7)^(1/4 + 1)/(1/4 + 1) + C
= (4x - 7)^(5/4)/(5/4) + C
= (4/5)(4x - 7)^(5/4) + C
Отже, загальний вигляд первісних функції f(x) є:
F(x) = (4/5)(4x - 7)^(5/4) + C, де C - довільна константа
Объяснение:
Первісна функція √√4x - 7.
qepen xx
Маємо функцію f(x) = √√4x - 7. Знайди загальний вигляд первісних. Загальний вигляд первісних функції:
Почнемо з використання підстановки u = √(4x - 7), тоді можна записати:
du/dx = 2 / √(4x - 7)
dx = (1/2) u / √(4x - 7) du
Тоді функція f(x) може бути переписана як:
f(x) = √u
f(x) = u^(1/2)
f(x) = (4x - 7)^(1/4)
Тому загальний вигляд первісних функції f(x) має вигляд:
F(x) = (4x - 7)^(1/4) + C
де C є довільною константою і представляє будь-яку константу інтегрування.