Предмет: Геометрия,
автор: alexkapa007
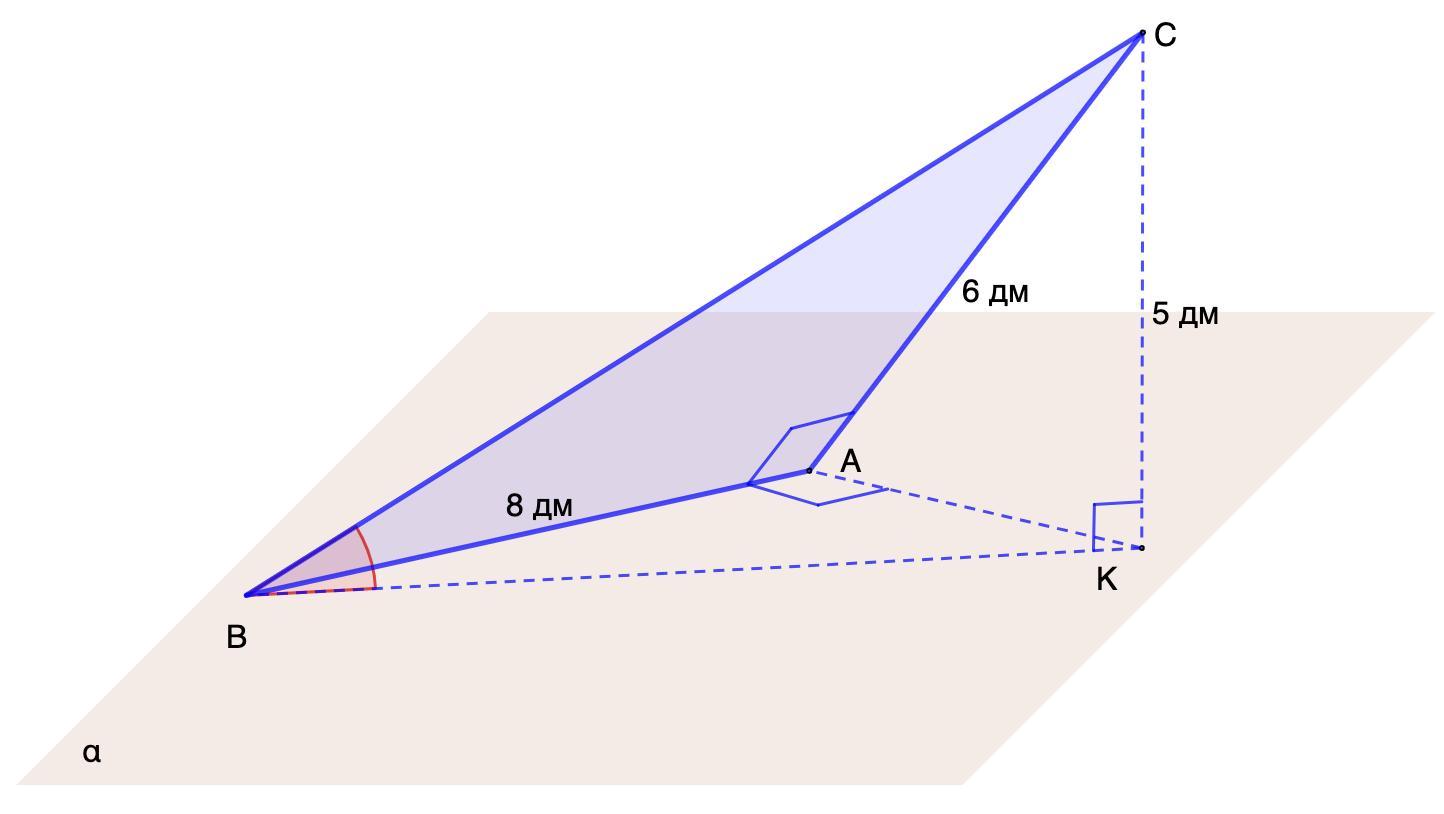
Через катет АВ прямокутного трикутника ABC (A = 90) проведено площину а. Знайдіть кут нахилу гіпотенузи до площини а, якщо АС = 6 дм, АВ - 8 дм, а точка С віддалена від площини а на 5 дм.
Ответы
Автор ответа:
1
Ответ:
Угол наклона гипотенузы к плоскости α равен 30°.
Объяснение:
Через катет АВ прямоугольного треугольника ABC (∠A = 90°) проведена плоскость α. Найдите угол наклона гипотенузы к плоскости α, если АС = 6 дм, АВ = 8 дм, а точка С удалена от плоскости α на 5 дм.
Дано: ΔАВС - прямоугольный; ∠А = 90°;
АВ ⊂ α; СК ⊥ α;
АС = 6 дм, АВ = 8 дм; СК = 5 дм.
Найти: угол наклона гипотенузы к плоскости α.
Решение:
- Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на плоскость.
СК ⊥ α ⇒ ВК - проекция ВС на α.
⇒ ∠СВК - искомый угол.
1. Рассмотрим ΔАВС - прямоугольный.
По теореме Пифагора найдем ВС:
ВС² = АВ² + АС² = 64 + 36 = 100 ⇒ ВС = √100 = 10 (дм)
2. Рассмотрим ΔВСК.
СК ⊥ α
- Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, принадлежащей этой плоскости.
⇒ СК ⊥ ВК ⇒ ΔВСК - прямоугольный.
- Синус угла - отношение противолежащего катета к гипотенузе.
⇒ ∠СВК = 30°
#SPJ1
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: victoriaboykoua
Предмет: Другие предметы,
автор: gomenukhristina2
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: Аноним