Найдите неизвестные размеры правильной четырёхугольной пирамиды. Помогите, пожалуйста! Нужно правильное решение)
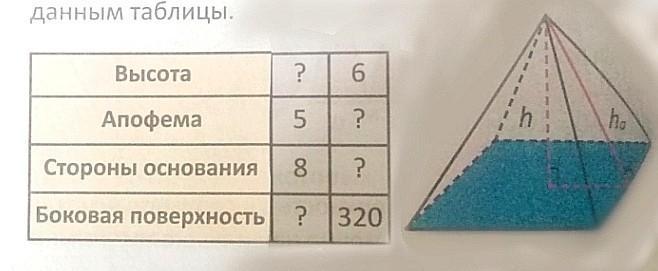
Ответы
Sбок = (1/2)PA.
1) Левая колонка. Р = 4а = 4*8 = 32.
Sбок = (1/2)32*5 = 80.
H = √(A² - (a/2)²) = √(25 – (8/2)²) = √(25 – 16) = √9 = 3.
2) Прпавая колонка.
2S = PA, p= 4a, aA = 2S/4 = S/2 = 320/2 = 160.
A = √((a/2)² + H²) = √((a²/4) + 36) = √(a² + 144)/2.
a*(√(a² + 144)/2)= 160.
a*√(a² + 144) = 320.
a²*(a² + 144) = 320².
a^4 + 144a² - 102400 = 0. Пусть a² = х.
Получаем квадратное уравнение х² + 144х – 102400 = 0.
D=144^2-4*1*(-102400)=20736-4*(-102400)=20736-(-4*102400)=20736-(-409600)=20736+409600=430336;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√430336-144)/(2*1)=(656-144)/2=512/2=256;
x_2=(-√430336-144)/(2*1)=(-656-144)/2=-800/2=-400.
Отрицательное значение отбрасываем (из него нельзя извлечь корень).
Находим а = √256 = 16.
Тогда А = √((а/2)² + Н²) = √(64 + 36) = √100 = 10.
