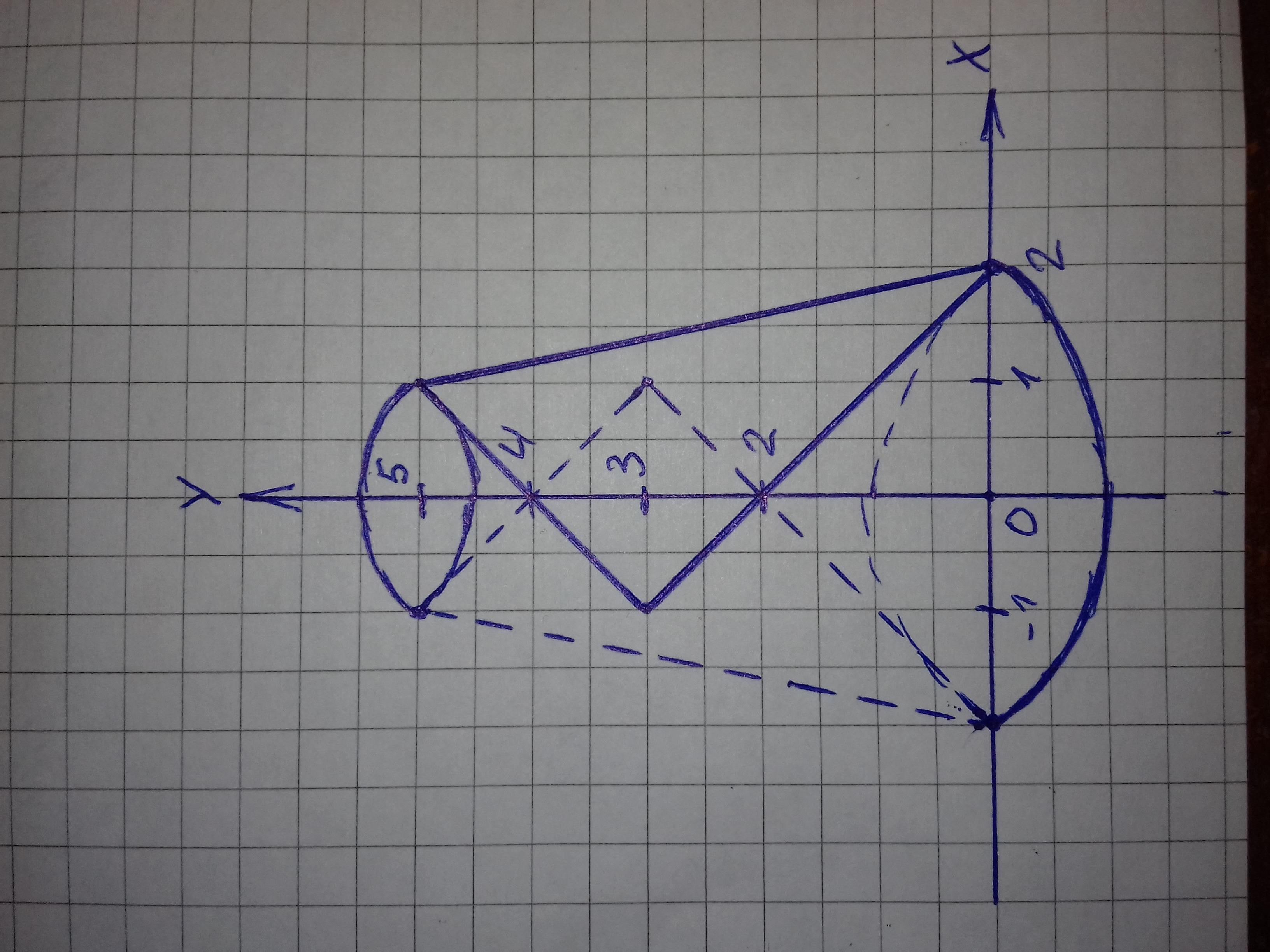
Треугольник с вершинами (2 ; 0) , (-1 ; 3) , (1;5) вращали вокруг оси y. Получилась объемная фигура. Чему равен ее объем ?
Ответы
Відповідь:
Объем фигуры Vф = pi/3 × 26 ≈ 27,2 см³.
Пояснення:
В результате вращения треугольника вокруг оси ОУ получили объемную фигуру. Фигура представляет собой усеченный конус с радиусом большего основания R2 = 2 см., радиусом меньшего основания R1 = 1 см. и высотой h = 5 см. В усеченном конусе есть два углубления в ввиде обычных конусов. Со стороны большего основания - конус с радиусом R2 = 2 см. и высотой h2 = 2 см. Со стороны меньшего основания - конус с радиусом R1 = 1 см. и высотой h1 = 1 см.
Используем следующие формулы:
1) объем усеченного конуса:
Vук = 1/3 × pi × ( R1² + R1R2 + R2²) × h
2) объем обычного конуса:
Vк = 1/3 × pi × R² × h
Объем фигуры, полученной в результате вращения треугольника вокруг оси ОУ равен объему усеченного конуса из которого вычтены объемы двух обычных конусов.
1) Объем усеченного конуса ( R2 = 2 см., R1 = 1 см., h = 5 см ):
Vук = 1/3 × pi × ( R1² + R1R2 + R2²) × h = pi/3 × ( 1² + 1 × 2 + 2² ) × 5 = pi/3 × 35 см³.
2) Объем верхнего конуса ( R2 = 2 см., h2 = 2 см. ):
Vк2 = 1/3 × pi × R2² × h2 = pi/3 × 2² × 2 = pi/3 × 8 см³.
3) Объем нижнего конуса ( R1 = 1 см., h1 = 1 см. ):
Vк1 = 1/3 × pi × R² × h = pi/3 × 1² × 1 = pi/3 см³.
Объем фигуры равен:
Vф = Vук - Vк1 - Vк2 = pi/3 × 35 - pi/3 - pi/3 × 8 = pi/3 × 26 ≈ 27,2 см³.