Предмет: Геометрия,
автор: starostenko231109
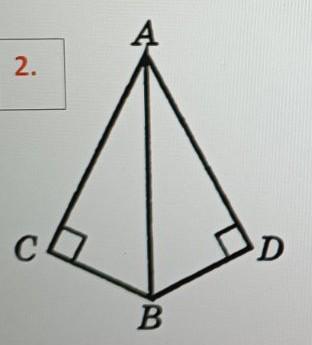
Прямокутні трикутники ABC i ABD мають спільну гіпотенузу АВ. Відомо, що AB бісектриса кута CAD. Доведіть, що BA - бісектриса кута CBD.
Допоможіть будь ласка
Приложения:
Ответы
Автор ответа:
5
Объяснение:
Рассмотрим задачу поэтапно и решим ее:
1. По условию задачи АВ биссектриса ∠CAD
(Напоминаю: биссектриса делит угол пополам)
→
∠CAB=∠DAB
Представим что эти углы равны х, тогда мы легко можем выразить углы CBA и BDA:
1) ∠CBA+∠BCA+∠CAB=180°
∠CBA+90°+x=180°
∠CBA=90°-x
2) ∠BDA+∠BDA+∠DAB=180°
∠BDA+90°+x=180°
∠BDA=90°-x
→
∠CBA= ∠BDA
→
AB биссектриса ∠CBD
Вот мы и доказали все, что требовалось в задаче)
Похожие вопросы
Предмет: Українська література,
автор: sevcenkoaleksandra91
Предмет: Физика,
автор: ketslilia201113
Предмет: Русский язык,
автор: ayaulym65
Предмет: Физика,
автор: nekitlitvinenko228
Предмет: Химия,
автор: kobetssofiya