Предмет: Геометрия,
автор: orkwkfir
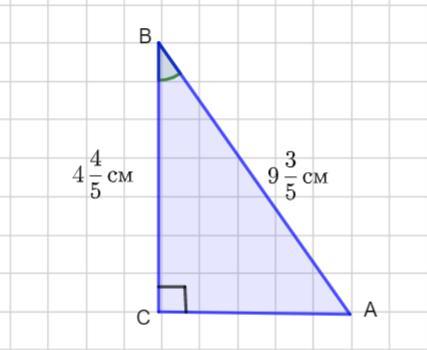
У трикутнику ABC кут С=90°, BC=4 4/5 см, AB=9 3/5 см. Знайдіть кут B.
Ответы
Автор ответа:
2
Ответ:
∠В =60°.
Объяснение:
В треугольнике АВС угол С =90 °, ВС = 4 4/5 см, АВ = 9 3/5 см. Найти угол В.
Пусть дан ΔАВС - прямоугольный, так как ∠С =90°.
Катет см , а гипотенуза
см.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе
Чтобы разделить одну дробь на другую, надо делимое умножить на дробь, обратную делителю.
Чтобы записать смешанное число в виде неправильной дроби можно:
- знаменатель умножить на целую часть;
- к произведению прибавить числитель дробной части;
- полученную сумму записать в числитель, а знаменатель оставить без изменений.
Тогда ∠В =60°.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Dorapomidora231
Предмет: Геометрия,
автор: irunchik16
Предмет: История,
автор: skonrad477
Предмет: Математика,
автор: Lisiy32654