Предмет: Геометрия,
автор: WOT000
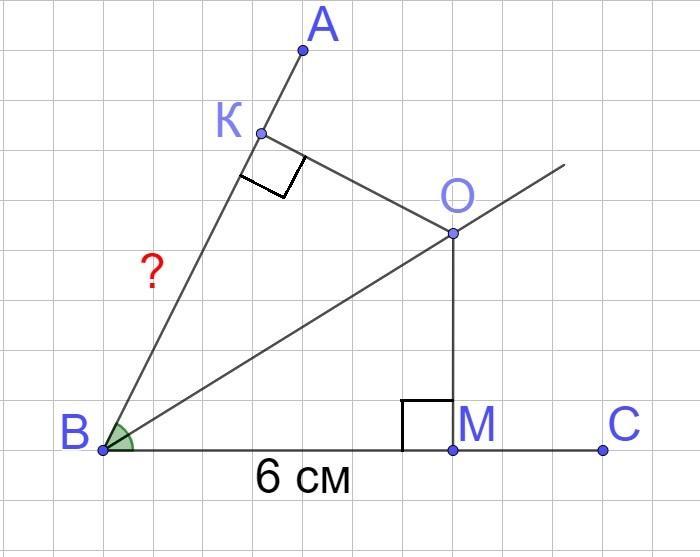
Із точки О, яка лежить на бісектрисі кута АВС, проведено перпендикуляри ОМ і ОК до його сторін. Знайдіть відрізок ВК, якщо ВМ = 6 см.
Ответы
Автор ответа:
4
Ответ:
Відрізок ВК дорівнює 6 см
Объяснение:
Із точки О, яка лежить на бісектрисі кута АВС, проведено перпендикуляри ОМ і ОК до його сторін. Знайдіть відрізок ВК, якщо ВМ = 6 см.
- Якщо гіпотенуза і гострий кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі та гострому куту іншого, то такі трикутники рівні.
Розглянемо трикутники ОМВ і ОКВ. За умовою ОМ⊥ВС, ОК⊥АВ, тому ∠ОМВ=∠ОКВ=90° ⇒ трикутники прямокутні.
ВО - бісектриса ∠АВС, тому ∠КВО=∠МВО.
Сторона ОВ (гіпотенуза трикутніків) - спільна.
Тому ΔОМВ=ΔОКВ за гіпотенузої і гострим кутом.
У рівних трикутників відповідні сторони рівні: ВК=ВМ=6 (см)
Відповідь: 6 см
#SPJ1
Приложения:
Мозгокошка:
Здравствуйте.Можете пожалуйста мне помочь?Я выложила в профиле задания по алгебре/геометрии.Пожалуйста,если у Вас есть время/возможность,то помогите.Хотя бы посмотрите,прошу.Была бы безумно благодарна.В любом случае спасибо Вам и доброго времени суток
Похожие вопросы
Предмет: Русский язык,
автор: jumabaeva444
Предмет: Алгебра,
автор: ivannazdanevic
Предмет: Математика,
автор: xrstmiroslava
Предмет: Литература,
автор: semyazyablovyh
Предмет: Геометрия,
автор: nastyaarmybp