Предмет: Математика,
автор: irmuxamedov19
Помогите пожалуйста срочно
Приложения:
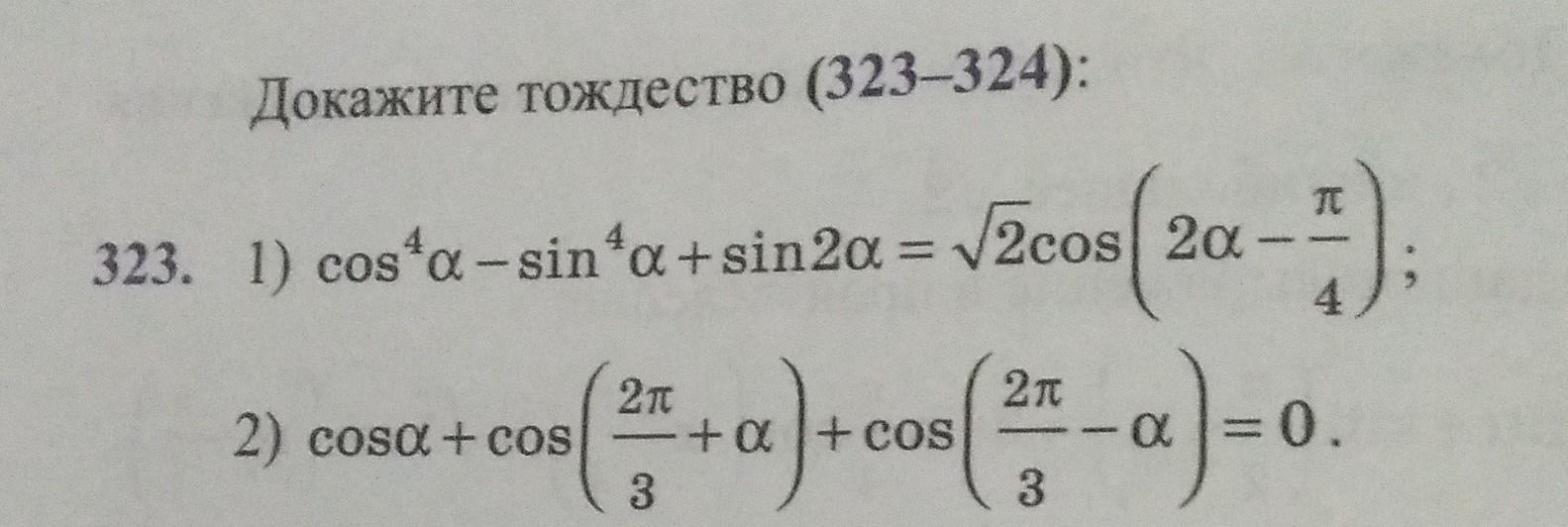
Ответы
Автор ответа:
0
Ответ:
Доказать тождества.
Применяем формулы суммы косинусов, косинуса двойного аргумента , разности квадратов .
masha01021:
здравствуйте помогите пожалуйста решить передел
Похожие вопросы
Предмет: Химия,
автор: o6863599
Предмет: Алгебра,
автор: goldilocks113
Предмет: Геометрия,
автор: TYuvelir
Предмет: Алгебра,
автор: viktorvechnyj
Предмет: Русский язык,
автор: alenamuradanc4272