Question

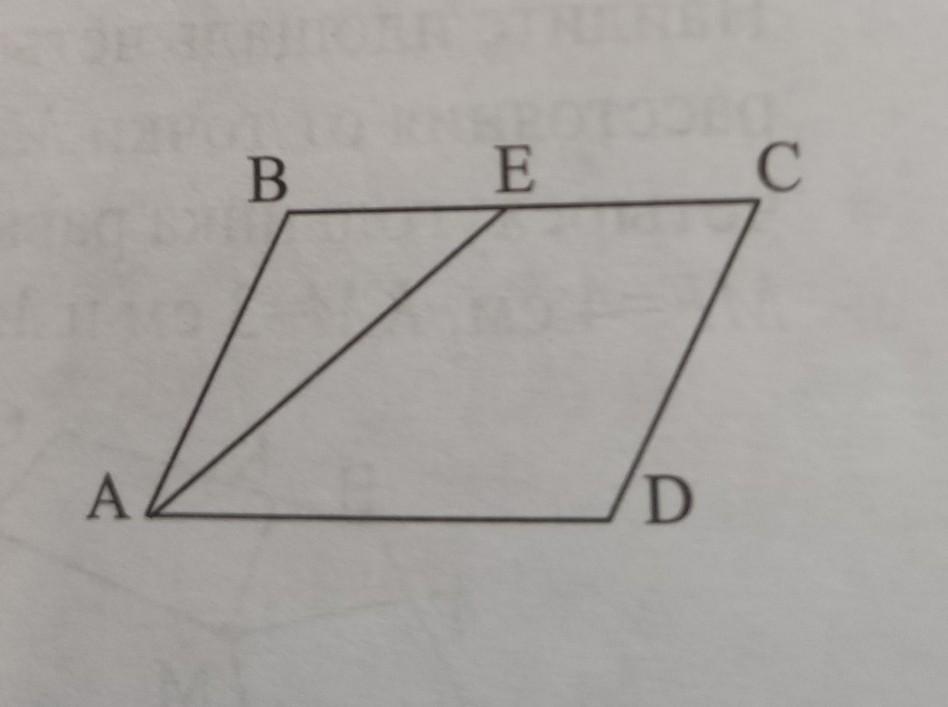
2. В параллелограмме ABCD с площадью 120 см² и периметром 36 см, AD=12 см, AE - биссектриса. Найдите площадь трапеции AECD. ​

Answer 1

Відповідь:

90 см²

Покрокове пояснення:

нехай сторони паралелограма a та b, висота h

a = 12 см (за умовою)

b = (36 - 12*2)/2 = (36-24)/2 =12/2= 6 (см)

h = 120/12 = 10 (см)

у трапеції: нижня основа дорівнює a = 12 см

висота дорівнює h = 10 см

верхня основа трапеції EC

BC точкою E ділиться на відрізки BE та EC

т.я. AD || BC, то угол DAE = углу BEA

т.я. AE - бісектриса, тоді кут DAE = куту BAE

у трикутник BAE кути BAE та BEA рівні => трикутник рівнобедрений, , отже  BE = AB = b = 6 см

верхня основа трапеції EC = 6 см

Sтрапеції = (12+6)*10/2 = (18*10)/2 = 180/2 = 90 (см²)

Ответ: 90 см²