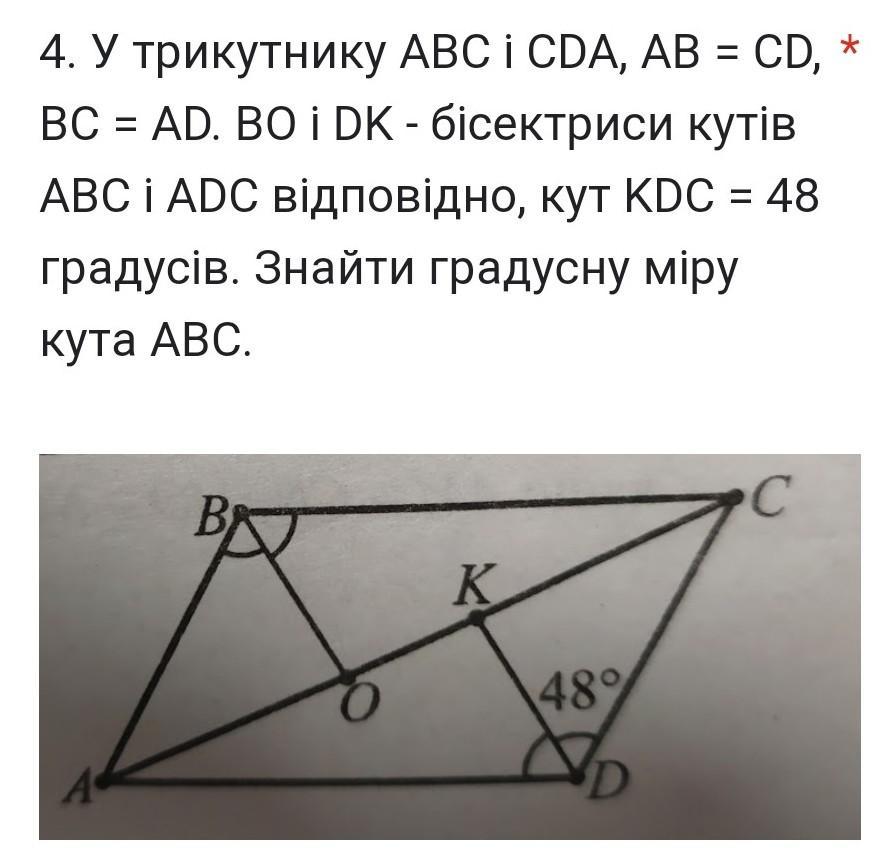
У трикутнику ABC i CDA, AB = CD, BC = AD. BO i DK - бісектриси кутів ABC i ADC відповідно, кут KDC = 48 градусів. Знайти градусну міру кута ABC.
Ответы
Дано: у трикутнику ABC і CDA, AB = CD, BC = AD; BO і DK - бісектриси кутів ABC і ADC відповідно; кут KDC = 48 градусів.
Потрібно знайти градусну міру кута ABC.
Розв'язок: оскільки AB = CD та BC = AD, то трикутники ABC та ADC є подібними за теоремою про бічний кут трикутника. Також бісектриси BO і DK є висотами у трикутниках ABC та ADC відповідно, оскільки вони перпендикулярні до протилежних сторін.
Отже, в трикутнику ABC і трикутнику ADC відповідні бічні сторони мають спільний кут при вершині C, а також мають однакові висоти BO і DK. Тому ці трикутники є подібними за пропорційністю бічних сторін і мають спільний кут при вершині C.
Звідси отримуємо, що кут ABC дорівнює куту ADC, оскільки вони є відповідними кутами подібних трикутників. З іншого боку, кут ADC дорівнює 180° - куту KDC - куту ACD = 180° - 48° - 1/2 * ABC, оскільки DK є бісектрисою кута ADC. Таким чином, маємо:
ABC = ADC = 180° - KDC - ACD = 180° - 48° - 1/2 * ABC - 1/2 * ABC = 84°.
Відповідь: кут ABC дорівнює 84 градусам.