Question

Основа трикутника дорівнює 30 см, а бічні сторони дорівнюють 26 і 28 см. Висота поділена у відношенні 2 : 3 (починаючи від вершини), і через точку поділу проведено пряму, паралельну основі. Знайти площу отриманої трапеції.

Answer 1

Ответ:

282,24 см²

Объяснение:

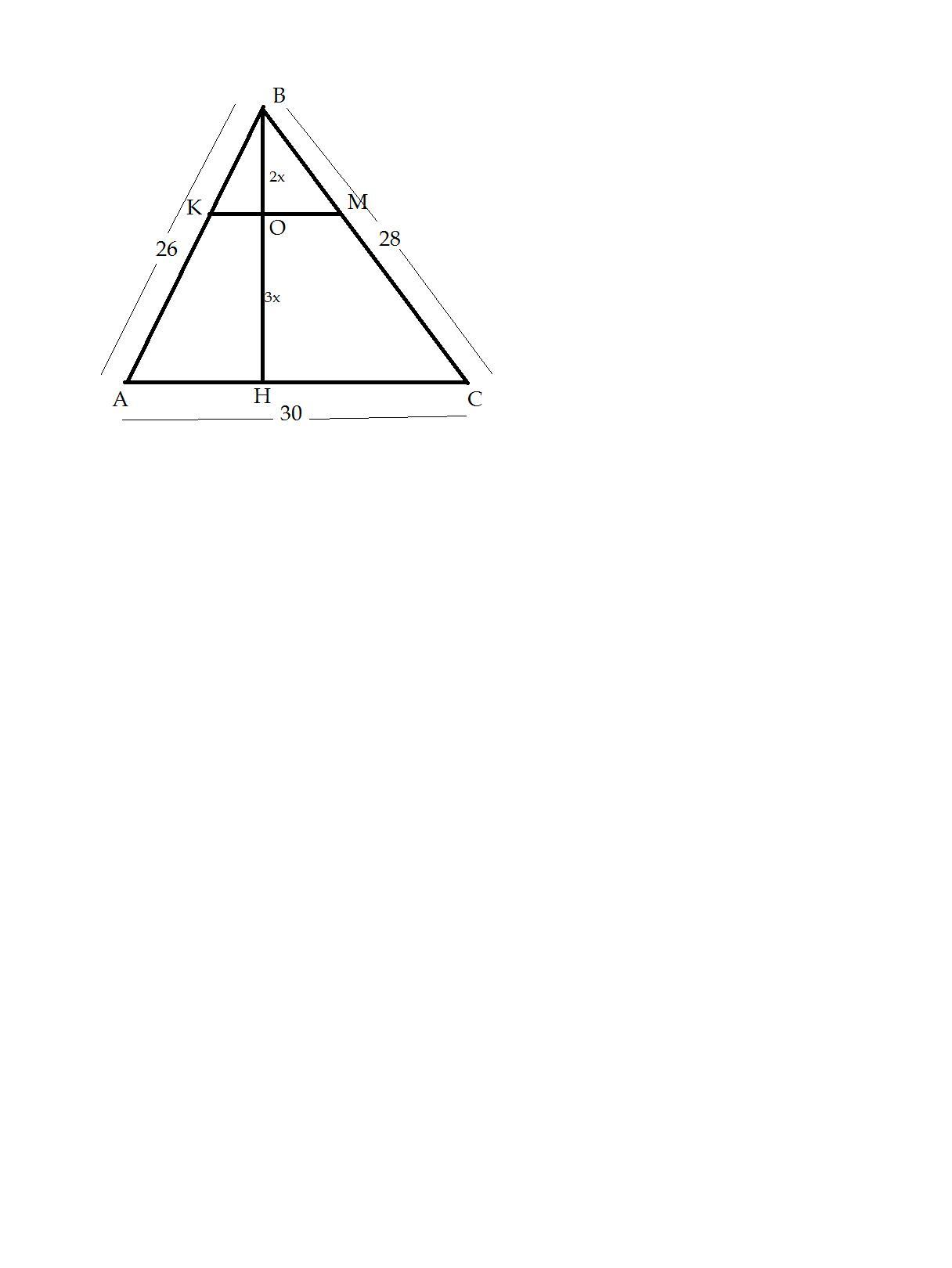
Дано: ΔАВС, АВ=26 см, ВС=28 см, АС=30 см.  КМ║АС;  ВН - висота;

ВО/ОН=2/3, S(АКМС) - ?

Знайдемо висоту ВН через площу ΔАВС.

За формулою Герона

S(ABC)=√(p(p-a)(p-b)(p-c), де р - півпериметр трикутника, а, b, c - його сторони

S=√(42*12*14*16)=√112896=336 cм²

S(ABC)=1/2 * AC * BH;  336=1/2 * 30 * ВН;  ВН=336:15=22,4 см.

КМ║АС, тому ΔКВМ подібний до ΔАВС за трьома кутами. Звідси

КМ/АС=ВО/ВН=2х/5х;  КМ=АС*ВО:ВН=30*2х:5х=12 см.

S(АКМС)=(КМ+АС)/2 * ОН;  ВО+ОН=2х+3х=22,4 см;  5х=22,4;  х=4,48;

ОН=4,48*3=13,44 см.

S(АКМС)=(12+30):2*13,44=282,24 см²