Обязательно с рисунком и пояснениями !
Дан угол , равный α , и треугольник ABC такой , что ∠A + ∠B = α. Найдите траекторию которую опишет вершина C , если вершины A и B будут скользить по сторонам угла
(Вершина угла и С расположены по разные стороны от АВ)
Ответы
Ответ:
Слишком длинный, чтобы помещать его сюда.
Объяснение:
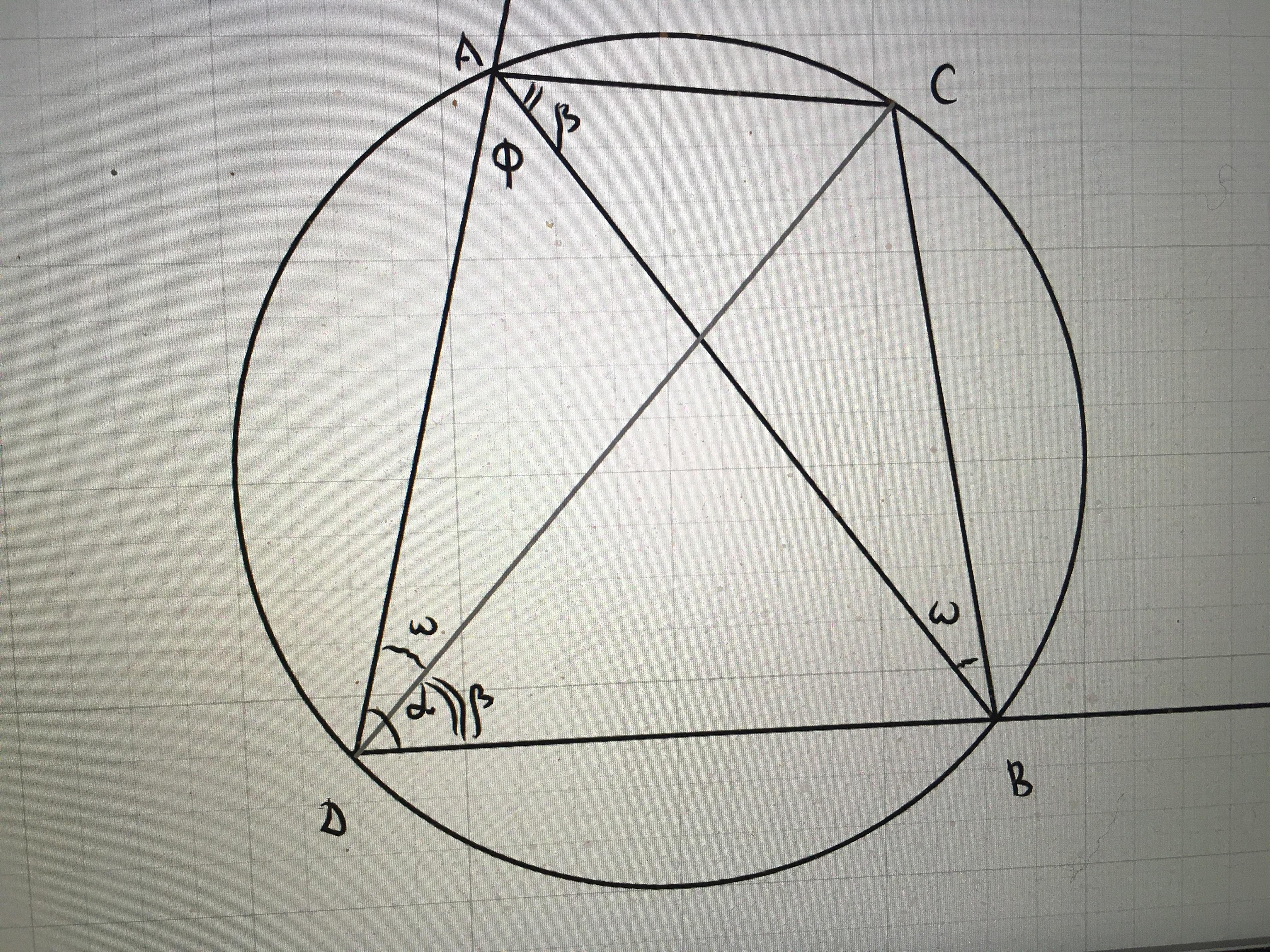
Обозначим вершину угла буквой D. Поскольку сумма углов в Δ равна 180°, и ∠A+∠B=∠β+∠ω=α=∠D⇒∠C=180-α; ∠B+∠D=180°⇒ вокруг четырехугольника DACB можно описать окружность⇒ вписанные в эту окружность углы BDC и BAC равны, поскольку опираются на одну и ту же дугу. Вывод: вершина C двигается по лучу с вершиной в точке D, который образует со сторонами данного угла углы, равные ∠A и ∠B. Надо понять, в каких пределах перемещается C.
Обратим внимание на то, что при любом расположении треугольника ABC, радиус окружности, описанной вокруг DACB, всё время один и тот же - ведь это же просто окружность, описанная вокруг треугольника ABC. Треугольник двигается, и окружность двигается, но при этом всё время проходит через D. Кстати, диаметр этой окружности может быть вычислен по теореме синусов:
Отсюда, кстати, получается оценка DC≤2R - ведь хорда не может быть больше диаметра. Чтобы узнать точные границы для y=DC, обозначим ∠ADB=Ф, тогда
при Ф+β=π/2, Ф=π/2-β; слева производная положительна, справа отрицательна. В точке максимума y=2R. При Ф=0 (это когда B=D)
y=2Rsin β;
при Ф=180°-α (это когда A=D)
y=2Rsin(180°-α+β)=2Rsin (180°-ω) =2Rsin ω.
Обозначим min(2Rsin β; 2Rsin ω)=m.
Тогда окончательный ответ такой: C двигается по лучу с вершиной в D, при этом расстояние между C и D меняется между m и 2R.
Замечание. Рассуждение корректно, если точка максимума π/2-β принадлежит интервалу (0; 180°-α). То есть если
90°-β>0 и 90°-β<180°-α;
β<90° и α-β<90°;
β<90° и ω<90°.
Если же один из этих углов больше или равен 90 градусов, расстояние меняется между 2Rsin β и 2Rsin ω. Конечно, это возможно только если сам угол α>90°.