Предмет: Алгебра,
автор: svlanko
помогите пожалуйста решить
Приложения:
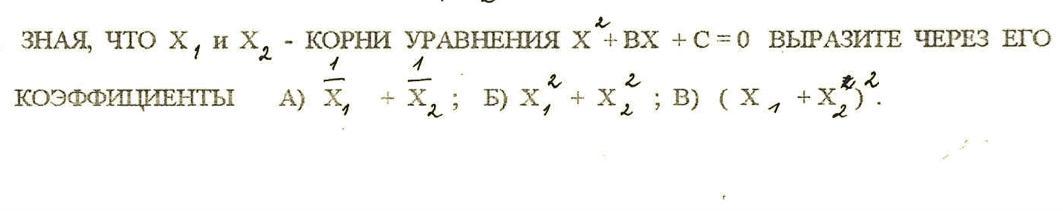
Ответы
Автор ответа:
1
Ответ:
А)
Б)
В)
Объяснение:
Зная, что х₁ и х₂ - корни уравнения х² + bx + c = 0, выразите через его коэффициенты:
А)
Б)
В)
- Теорема Виета:
- Сумма корней приведенного квадратного уравнения x² + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.
х₁ + х₂ = -b; x₁ · x₂ = c
А)
Приведем к общему знаменателю:
Б)
Дополним до полного квадрата, для этого прибавим и отнимем 2х₁х₂:
В)
Здесь просто заменим выражение в скобках на (-b):
Похожие вопросы
Предмет: Математика,
автор: nazarzorin9
Предмет: Українська мова,
автор: galilejartur
Предмет: Українська мова,
автор: Аноним
Предмет: Математика,
автор: miniboss07