Question

ТЕРМІНОВО ПОТРІБНА ДОПОМОГА! МАТЕМАТИКА, 11 КЛАС. ОБ'ЄМИ ТІЛ.
ЗАВДАННЯ 3

Answer 1

Ответ:

Высота правильной четырехугольной пирамиды $\displaystyle \frac{3\sqrt{3}\sqrt[4]{3} }{2}$  (см)

Пошаговое объяснение:

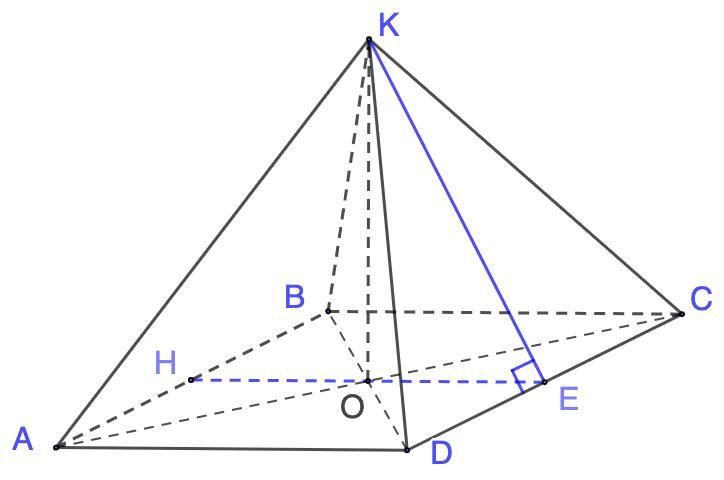
3. Найдите высоту правильной четырехугольной пирамиды, площадь боковой поверхности которой равна 60√3 см², а площадь полной поверхности 108√3 см².

Дано: KABCD - правильная пирамида,

Sбок = 60√3 см²;

Sполн =  108√3 см²

Найти: КО.

Решение:

Площадь полной поверхности пирамиды равна:

Sполн = Sбок + Sосн

⇒ Sосн = Sполн - Sбок = 108√3 - 60√3 = 48√3 (см²)

В основании правильной пирамиды лежит квадрат.

Пусть сторона квадрата равна а.

Площадь квадрата равна:

S = a²,

где а - сторона квадрата.

Sосн = S(ABCD) = а² = 48√3 (см²)

⇒  $\displaystyle a=\sqrt{48\sqrt{3} }= 4\sqrt{3\sqrt{3} }$ (см)

$\displaystyle OE=a:2=2\sqrt{3\sqrt{3} }$ (см)

Площадь боковой поверхности равна:

Sбок = 0,5 · Росн · l,

где l - апофема.

Периметр основания равен:

Росн = 4а = $\displaystyle 16\sqrt{3\sqrt{3} }$  (см)

Подставим значения:

$\displaystyle 60\sqrt{3}=\frac{1}{2}\cdot 16\sqrt{3}\cdot \sqrt{\sqrt{3} } \cdot KE\\\\KE=\frac{60\sqrt{3} }{8\sqrt{3}\sqrt{\sqrt{3} } } =\frac{15}{2\sqrt{\sqrt{3} } }$

Рассмотрим ΔОКЕ - прямоугольный.

По теореме Пифагора найдем ОК:

ОК² = KE² - OE²

$\displaystyle OK^2=\frac{225}{4\sqrt{3} } -4\cdot 3\sqrt{3} =\frac{225-48\cdot3}{4\sqrt{3} }=\frac{81\cdot \sqrt{3} }{4\cdot3} =\frac{27\sqrt{3} }{4}$

⇒ $\displaystyle OK=\frac{3\sqrt{3}\cdot\sqrt{\sqrt{3} } }{2} =\frac{3\sqrt{3}\sqrt[4]{3} }{2}$  (см)