Предмет: Алгебра,
автор: dolmatkz01
23.12. Докажите тождество: 1) tgx + tg(180°- x) + ctg(360°-x) = ctg(180°- x); 2) ctgx + tg(90° + x) + tg(360° + x) = ctg(270°- x); + B). B). etg ( 2 Зл 2 3) sin 23,13. Упростит - B) B + sin(180° - B) + ctg 3 T 2 B = tgß. =
Приложения:
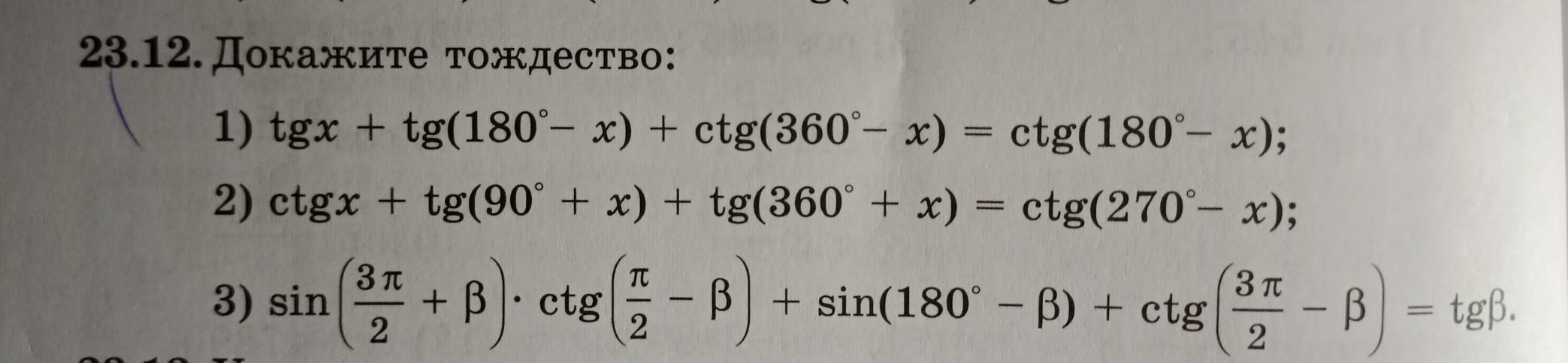
Ответы
Автор ответа:
5
1) tgx + tg(180°-x) + ctg(360°-x) = ctg(180°-x)
По формулам приведения
tg(180°-x) = -tgx
ctg(360°-x) = -ctgx
ctg(180°-x) = -ctgх
Мы получаем:
tgx + (-tgx) + (-ctgx) = -ctgx
0 + (-ctgx) = -ctgx
-ctgx = -ctgx
Доказано!
2) ctgx + tg(90°+x) + tg(360°+x) = ctg(270°-x)
Тоже используем формулы приведения
tg(90°+x) = -ctgx
tg(360°+x) = tgx
ctg(270°-x) = tgx
Таким образом:
ctgx + (-ctgx) + tgx = tgx
0 + tgx = tgx
tgx = tgx
Доказано!
3) sin(3π/2+β) · ctg(π/2-β) + sin(180°-β) + ctg(3π/2-β) = tgβ
По формулам
sin(3π/2+x) = -cosx
ctg(π/2-x) = tgx
sin(180°-x) = sinx
ctg(3π/2-x) = tgx
Получаем:
-cosβ · tgβ + sinβ + tgβ = tgβ
Используем тригонометрическое тождество tgx = sinx/cosx :
-cosβ · (sinβ/cosβ) + sinβ + tgβ = tgβ
-sinβ + sinβ + tgβ = tgβ
tgβ = tgβ
Доказано!
#SPJ1
Похожие вопросы
Предмет: Математика,
автор: erasylamanbek650
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: Аноним
Предмет: Русский язык,
автор: diliarasaginova